题目内容
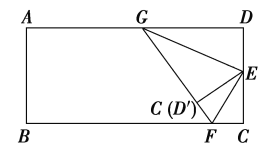
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
【答案】C
【解析】试题分析:①利用线段垂直平分线的性质的逆定理可得结论;②证△OMB≌△OEB得△EOB≌△CMB;
③先证△BEF是等边三角形得出BF=EF,再证DEBF得出DE=BF,所以得DE=EF;④由②可知△BCM≌△BEO,则面积相等,△AOE和△BEO属于等高的两个三角形,其面积比就等于两底的比,即S△AOE:S△BOE=AE:BE,由直角三角形30°角所对的直角边是斜边的一半得出BE=2OE=2AE,得出结论S△AOE:S△BOE=AE:BE=1:2.
①∵矩形ABCD中,O为AC中点, ∴OB=OC, ∵∠COB=60°, ∴△OBC是等边三角形, ∴OB=BC,
∵FO=FC, ∴FB垂直平分OC, 故①正确;
②∵FB垂直平分OC, ∴△CMB≌△OMB, ∵OA=OC,∠FOC=∠EOA,∠DCO=∠BAO, ∴△FOC≌△EOA,
∴FO=EO, 易得OB⊥EF, ∴△OMB≌△OEB, ∴△EOB≌△CMB, 故②正确;
③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°,BF=BE, ∴△BEF是等边三角形, ∴BF=EF,
∵DF∥BE且DF=BE, ∴四边形DEBF是平行四边形, ∴DE=BF, ∴DE=EF, 故③正确;
④在直角△BOE中∵∠3=30°, ∴BE=2OE, ∵∠OAE=∠AOE=30°, ∴AE=OE, ∴BE=2AE,
∴S△AOE:S△BCM=S△AOE:S△BOE=1:2, 故④错误;
所以其中正确结论的个数为3个

 名校课堂系列答案
名校课堂系列答案