题目内容
【题目】如图(a),将两块直角三角尺的直角顶点C叠放在一起.
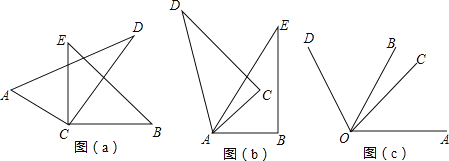
(1)若∠DCE=35°,∠ACB= ;若∠ACB=140°,则∠DCE= ;并猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
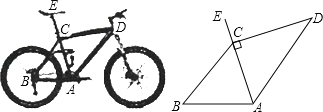
(2)如图(b),若是两个同样的三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小有何关系,请说明理由;
(3)已知∠AOB=α,∠COD=β(都是锐角),如图(c),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC的大小相等的关系(用含有α,β的式子表示).
【答案】(1)145°,40°,∠ACB+∠DCE=180°,理由见解析;(2)∠DAB+∠CAE=120°,理由见解析;(3)∠AOD+∠BOC=α+β.
【解析】
(1)若∠DCE=35°,根据90°计算∠ACE的度数,再计算∠ACB的度数;若∠ACB=140°,同理,反之计算可得结果;先计算∠ACB=90°+∠BCD,再加上∠DCE可得∠ACB与∠DCE的关系;
(2)先计算∠DAB=60°+∠CAB,再加上∠CAE可得结果;
(3)先计算∠AOD=β+∠COA,再加上∠BOC可得结果.
解:(1)若∠DCE=35°,
∵∠ACD=90°,∠DCE=35°,
∴∠ACE=90°35°=55°,
∵∠BCE=90°,
∴∠ACB=∠ACE+∠BCE=55°+90°=145°;
若∠ACB=140°,
∵∠BCE=90°,
∴∠ACE=140°90°=50°,
∵∠ACD=90°,
∴∠DCE=90°50°=40°,
故答案为:145°;40°;
∠ACB+∠DCE=180°,
理由:∵∠ACB=∠ACD+∠BCD=90°+∠BCD,
∴∠ACB+∠DCE=90°+∠BCD+∠DCE=90°+∠BCE=180°;
(2)∠DAB+∠CAE=120°,
理由:∵∠DAB=∠DAC+∠CAB=60°+∠CAB,
∴∠DAB+∠CAE=60°+∠CAB+∠CAE=60°+∠EAB=120°;
(3)∠AOD+∠BOC=α+β,
理由:∵∠AOD=∠DOC+∠COA=β+∠COA,
∴∠AOD+∠BOC=β+∠COA+∠BOC=β+∠AOB=α+β.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案【题目】将连续的奇数1,3,5,7,……排成如下表:如图所示,图中的T字框框住了四个数字,若将T字框上下左右移动,按同样的方式可框住另外的四个数.
1 | 3 | 5 | 7 | 9 |
11 | 13 | 15 | 17 | 19 |
21 | 23 | 25 | 27 | 29 |
31 | 33 | 35 | 37 | 39 |
… | … | … | … | … |
(1)设T字框内处于中间且靠上方的数是整个数表当中从小到大排列的第n个数,请你用含n的代数式表示T字框中的四个数的和;
(2)若将T字框上下左右移动,框住的四个数的和能等于2020吗?如能,写出这四个数,如不能,说明理由.