Question

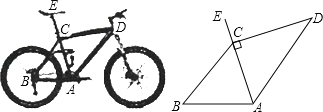
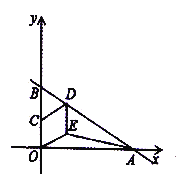
【题目】如图，Rt△ABC中，分别以AB、AC为斜边，向△ABC的内侧作等腰Rt△ABE、Rt△ACD，点M是BC的中点，连接MD、ME.

（1）若AB＝8，AC＝4，求DE的长；

（2）求证：AB－AC＝2DM.

Answer 1

【答案】（1）；（2）证明见解析.

【解析】

试题（1）根据三角函数求得AE和AD的长，二者的差就是所求.

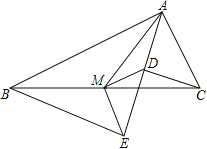
（2）延长CD交AB于点F，证明MD是△BCF的中位线，AF=AC，据此即可证得．

（1）直角△ABE中，AE=AB=，

在直角△ACD中，AD=AC=，

则DE=AE-AD=-=.

如图，延长CD交AB于点F．

在△ADF和△ADC中，∠FAD＝∠CAD，AD＝AD，∠ADF＝∠ADC，∴△ADF≌△ADC（ASA）.∴AC=AF，CD=DF.

又∵M是BC的中点，∴DM是△CBF的中位线.∴DM=BF=（AB-AF）=（AB-AC）.

∴AB-AC=2DM．