题目内容
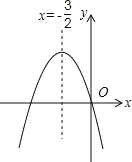
【题目】如图,已知抛物线![]() 与
与![]() 轴的一个交点
轴的一个交点![]() .
.
(1)试分别求出这条抛物线与![]() 轴的另一个交点
轴的另一个交点![]() 及与
及与![]() 轴的交点
轴的交点![]() 的坐标.
的坐标.
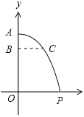
(2)设抛物线的顶点为![]() ,请在图中画出抛物线的草图,若点
,请在图中画出抛物线的草图,若点![]() 在直线
在直线![]() 上,试判断
上,试判断![]() 点是否在经过
点是否在经过![]() 点的反比例函数的图象上,并说明理由;
点的反比例函数的图象上,并说明理由;
(3)试求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
(1)把A点的坐标代入抛物线的解析式,就可以求出m的值,得到抛物线的解析式.在解析式中令y=0,解方程就可以求出与x轴的交点;(2)根据函数解析式就可求出抛物线的顶点坐标,利用待定系数法求出反比例函数的解析式.经过C,B的直线解析式可以用待定系数法求得,进而求出E点的坐标.把E的坐标代入反比例函数解析式,就可以判断是否在反比例函数的图象上;(3)过D作DF⊥y轴于点F,则△CFD为等腰直角三角形,△AOC是等腰直角三角形,根据勾股定理就可以求出CD,AC的长度.Rt△ADC中根据三角函数的定义就可以求出三角函数值.
解:(1)因为![]() 在抛物线
在抛物线![]() 上,
上,
则![]() ,解得
,解得![]() .
.
所以抛物线的解析式为![]() .
.
因为![]() 点为抛物线与
点为抛物线与![]() 轴的交点,求得
轴的交点,求得![]() ,
,
因为![]() 点为抛物线与
点为抛物线与![]() 轴的交点,求得
轴的交点,求得![]() .
.
(2)∵![]() ,
,
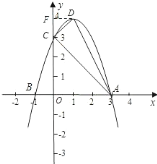
∴顶点![]() ,
,
画这个函数的草图.
由![]() ,
,![]() 点的坐标可求得直线
点的坐标可求得直线![]() 的解析式为
的解析式为![]() ,
,
∵点![]() 在
在![]() 上,
上,
∴![]() .
.
可求得过![]() 点的反比例函数的解析式为
点的反比例函数的解析式为![]() .
.
当![]() 时,
时,![]() .
.
∴点![]() 不在过
不在过![]() 点的反比例函数图象上.
点的反比例函数图象上.
(3)过![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() .
.
连接![]() ,则
,则![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() .
.
因为![]() ,
,
∴![]() 中,
中,![]() .
.
另解:∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.

练习册系列答案
相关题目