题目内容
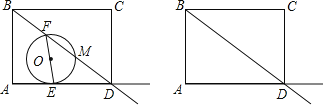
【题目】如图,在正方形![]() 中,
中,![]() 是
是![]() 边上的一点,
边上的一点,![]() ,
,![]() ,将正方形边
,将正方形边![]() 沿
沿![]() 折叠到
折叠到![]() ,延长
,延长![]() 交
交![]() 于
于![]() .连接
.连接![]() ,现在有如下四个结论:①
,现在有如下四个结论:①![]() ;②
;②![]() ;③
;③![]() ∥
∥![]() ;④
;④![]() ; 其中结论正确的个数是( )
; 其中结论正确的个数是( )
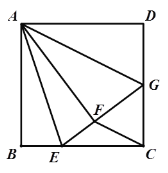
A.1B.2
C.3D.4
【答案】B
【解析】
①正确.证明Rt△AGD≌Rt△AGF,得到∠GAF=∠GAD,结合∠EAB=∠EAF可得结果.
②错误.可以证明DG=GC=FG,显然△GFC不是等边三角形,可得结论.
③正确.证明CF⊥DF,AG⊥DF即可.
④错误.证明FG:EG=3:5,求出△ECG的面积即可.
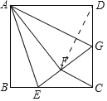
解:如图,连接DF.
∵四边形ABC都是正方形,
∴AB=AD=BC=CD,∠ABE=∠BAD=∠ADG=∠ECG=90°,
由翻折可知:AB=AF,∠ABE=∠AFE=∠AFG=90°,BE=EF=4,∠BAE=∠EAF,
∵∠AFG=∠ADG=90°,AG=AG,AD=AF,
∴Rt△AGD≌Rt△AGF(HL),
∴DG=FG,∠GAF=∠GAD,设GD=GF=x,
∴∠EAG=∠EAF+∠GAF=![]() (∠BAF+∠DAF)=45°,故①正确,
(∠BAF+∠DAF)=45°,故①正确,
在Rt△ECG中,∵EG2=EC2+CG2,
∴(4+x)2=82+(12x)2,
∴x=6,
∵CD=BC=BE+EC=12,
∴DG=CG=6,
∴FG=GC,
易知△GFC不是等边三角形,显然FG≠FC,故②错误,
∵GF=GD=GC,
∴∠DFC=90°,
∴CF⊥DF,
∵AD=AF,GD=GF,
∴AG⊥DF,
∴CF∥AG,故③正确,
∵S△ECG=![]() ×6×8=24,FG:FE=6:4=3:2,
×6×8=24,FG:FE=6:4=3:2,
∴FG:EG=3:5,
∴S△GFC=![]() ×24=
×24=![]() ,故④错误,
,故④错误,
故选B.

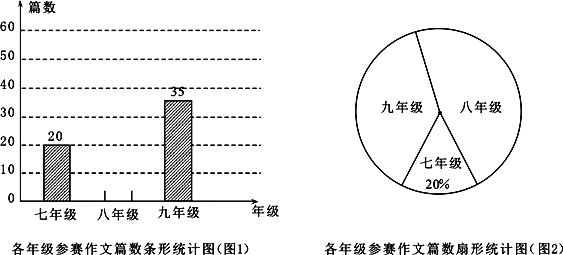
【题目】为了传承中华优秀传统文化,某校组织八年级学生参加了“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,绘制如下不完整的条形统计图.
汉字听写大赛成绩分数段统计表
分数段 | 频数 |
| 2 |
| 6 |
| 9 |
| 18 |
| 15 |
汉字听写大赛成绩分数段条形统计图

(1)补全条形统计图.
(2)这次抽取的学生成绩的中位数在________的分数段中;这次抽取的学生成绩在![]() 的分数段的人数占抽取人数的百分比是_______.
的分数段的人数占抽取人数的百分比是_______.
(3)若该校八年级一共有学生350名,成绩在90分以上(含90分)为“优”,则八年级参加这次比赛的学生中成绩“优”等的约有多少人?