题目内容
如图,点E、F分别是正方形纸片ABCD的边BC、CD上一点,将正方形纸片ABCD分别沿AE、AF折叠,使得点B、D恰好都落在点G处,且EG=2,FG=3,则正方形纸片ABCD的边长为______.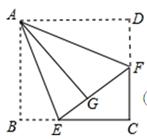

6
试题分析:设正方形ABCD的边长为x,根据翻折变换的知识可知BE=EG=2,DF=GF=3,则EC=x-2,FC=x-3,在Rt△EFC中,根据勾股定理列出式子即可求得边长x的长度.
设正方形ABCD的边长为x,
根据折叠的性质可知:BE=EG=2,DF=GF=3,
则EC=x-2,FC=x-3,
在Rt△EFC中,EC2+FC2=EF2,
即(x-2)2+(x-3)2=(2+3)2,
解得:x1=6,x2=-1(舍去),
故正方形纸片ABCD的边长为6.
点评:解答本题的关键是熟练掌握翻折变换的性质:翻折前后对应边相等,另外要求同学们熟练掌握勾股定理的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目