题目内容
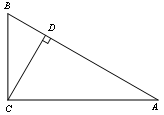
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D.则△BCD与△ABC的周长之比为( )
A.1︰2 B.1︰3 C.1︰4 D.1︰5

A.1︰2 B.1︰3 C.1︰4 D.1︰5
A
试题分析:易证得△BCD∽△BAC,得∠BCD=∠A=30°,那么BC=2BD,即△BCD与△BAC的相似比为1:2,根据相似三角形的周长比等于相似比即可得到正确的结论.
∵∠B=∠B,∠BDC=∠BCA=90°,
∴△BCD∽△BAC;①
∴∠BCD=∠A=30°;
Rt△BCD中,∠BCD=30°,则BC=2BD;
由①得:C△BCD:C△BAC=BD:BC=1:2;
故选A.
点评:解题的关键是熟练掌握相似三角形的性质:相似三角形的周长比等于相似比,面积比等于相似比的平方.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
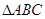 中,
中,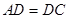 ,
,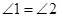 ,则
,则