题目内容
如图,AB的中垂线为CP交AB于点P,且AC =2CP.甲、乙两人想在AB上取D、E两点,使得AD=DC=CE=EB,其作法如下:甲作ÐACP、ÐBCP的角平分线,分别交AB于D、E两点,则D、E即为所求;乙作AC、BC的中垂线,分别交AB于D、E两点,则D、E即为所求.对于甲、乙两人的作法,下列正确的是( ).
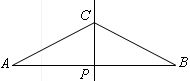
A. 两人都正确 B. 两人都错误
C.甲正确,乙错误 D. 甲错误,乙正确

A. 两人都正确 B. 两人都错误
C.甲正确,乙错误 D. 甲错误,乙正确
D
试题分析:根据直线CP是AB的中垂线且交AB于P,判断出△ABC是等腰三角形,即AC=BC,再根据线段垂直平分线的性质作出AD=DC=CE=EB.
甲:虽然CP=
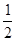 AP,
AP,但∠A≠
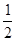 ∠ACP,
∠ACP,即∠A≠∠ACD.
乙:∵CP是线段AB的中垂线,
∴△ABC是等腰三角形,即AC=BC,∠A=∠B,
作AC、BC之中垂线分别交AB于D、E,
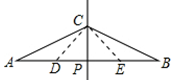
∴∠A=∠ACD,∠B=∠BCE,
∵∠A=∠B,
∴∠A=∠ACD,∠B=∠BCE,
∵AC=BC,
∴△ACD≌△BCE,
∴AD=EB,
∵AD=DC,EB=CE,
∴AD=DC=EB=CE.
所以甲错误,乙正确
故选D.
点评:解题的关键是熟练掌握垂直平分线的性质:垂直平分线上的点到线段两端的距离相等.

练习册系列答案
相关题目
 的面积是( )
的面积是( )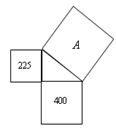

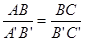 ;⑵
;⑵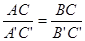 ③∠A=∠
③∠A=∠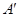 ;④∠C=∠
;④∠C=∠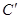
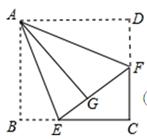
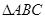 是等腰直角三角形,
是等腰直角三角形,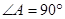 ,
,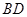 平分
平分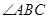 交
交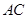 于点
于点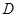 ,
,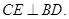
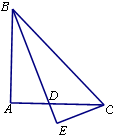
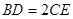 .
.