Question

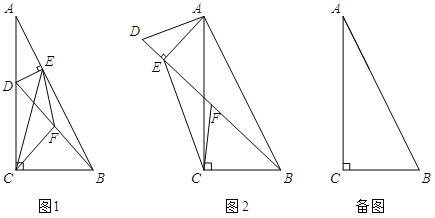
【题目】如图，已知在△ABC中，∠A=90°．

（1）请用圆规和直尺作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切（保留作图痕迹，不写作法和证明）；

（2）在（1）的条件下，若∠B=45°，AB=1，⊙P切BC于点D，求劣弧的长．

Answer 1

【答案】（1）画图见解析；（2）（2）弧AD的长为π.

【解析】分析: （1）作∠ABC的平分线，与AC的交点就是圆心P，此时⊙P与AB，BC两边都相切；如图，作BC的垂线PD，证明PD和半径相等即可，根据角平分线的性质可得：PA＝PD．

（2）要想求劣弧AD的长，根据弧长公式需求圆心角∠APD的半径AP的长，利用四边形的内角和求∠APD＝135°，再利用勾股定理和等腰三角形的性质求出AP＝PD＝DC＝1，代入公式可求弧长．

详解:

（1）作∠ABC的角平分线交AC于点P，以点P为圆心，AP为半径作圆.

（2）如图，∵P与AB，BC两边都相切，

∴∠BAP=∠BDP=90°，

∵∠ABC=45°，

∴∠APD=360°90°90°45°=135°，

∴∠DPC=45°，

∴△DPC是等腰直角三角形，

∴DP=DC，

在Rt△ABC中，AB=AC=1，

∴CB=，

∵BP=BP，AP=PD，

∴Rt△ABP≌Rt△DBP，

∴BD=AB=1，

∴CD=PD=AP=1，

∴劣弧AD的长==.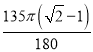

点睛: 本题考查了切线的判定、圆的作图以及弧长的计算，首先掌握切线的判定方法：①无交点，作垂线段，证半径；②有交点，作半径，证垂直；本题利用了第①种判定方法；并熟练掌握弧长计算公式：l＝（弧长为l，圆心角度数为n，圆的半径为R）．