题目内容
已知二次函数y=x2–kx+k–1(k>2).
(1)求证:抛物线y=x2–kx+k-1(k>2)与x轴必有两个交点;
(2)抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,若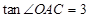 ,求抛物线的表达式;
,求抛物线的表达式;
(3)以(2)中的抛物线上一点P(m,n)为圆心,1为半径作圆,直接写出:当m取何值时,x轴与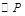 相离、相切、相交.
相离、相切、相交.
(1)证明详见解析;(2) ;(3)当
;(3)当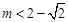 或
或 时,x轴与
时,x轴与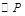 相离.;
相离.;
当 或
或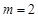 或
或 时,x轴与
时,x轴与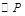 相切; 当
相切; 当 或
或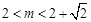 时,x轴与
时,x轴与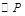 相交.
相交.
解析试题分析:(1)令y=0,得到一个关于字母x的一元二次方程,求出此方程的判别式的值为 ,根据k>2,可得
,根据k>2,可得
 ,即可得到答案.
,即可得到答案.
(2)令 ,有
,有 ;解得:
;解得: . 根据k的取值以及点A、B的位置确定
. 根据k的取值以及点A、B的位置确定 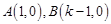 ;由抛物线与y轴交于点C得:
;由抛物线与y轴交于点C得: ;根据Rt
;根据Rt 中∠OAC的正切值求得k的取值,进而可得抛物线的表达式.(3)根据直线与圆的位置关系是由圆心到直线的距离和圆的半径确定的,当⊙P与x轴相切时,即y=±1;根据相切时m的取值即可作出判断,注意分类讨论.
中∠OAC的正切值求得k的取值,进而可得抛物线的表达式.(3)根据直线与圆的位置关系是由圆心到直线的距离和圆的半径确定的,当⊙P与x轴相切时,即y=±1;根据相切时m的取值即可作出判断,注意分类讨论.
试题解析:
(1)证明:∵
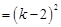 ,
,
又∵ ,
,
∴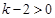 .
.
∴ 即
即 .
.
∴抛物线y = x2 – kx + k - 1与x轴必有两个交点.
(2) 解:∵抛物线y = x2 – kx + k -1与x轴交于A、B两点,
∴令 ,有
,有 .
.
解得: .
.
∵ ,点A在点B的左侧,
,点A在点B的左侧,
∴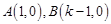 .
.
∵抛物线与y轴交于点C,
∴ .
.
∵在Rt 中,
中, 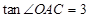 ,
,
∴ , 解得
, 解得 .
.
∴抛物线的表达式为 .
.
(3)解:当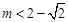 或
或 时,x轴与
时,x轴与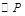 相离.
相离.
当 或
或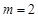 或
或 时,x轴与
时,x轴与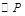 相切.
相切.
当 或
或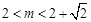 时,x轴与
时,x轴与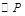 相交.
相交.
考点:1、根的判别式;2、求二次函数的解析式;3、直线与圆的位置关系.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目

 的图象开口向上,并且经过原点
的图象开口向上,并且经过原点
 .
. 的值;
的值; 与x轴的两个交点分别为A(1,0)和B(3,0),与y轴交于点C.
与x轴的两个交点分别为A(1,0)和B(3,0),与y轴交于点C.
 .
.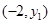 与
与 在此二次函数的图象上,则
在此二次函数的图象上,则
 (填 “>”、“=”或“<”);
(填 “>”、“=”或“<”); ,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.

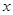 天后每千克该野生菌的市场价格为y元,试写出y与x之间的函数关系式;
天后每千克该野生菌的市场价格为y元,试写出y与x之间的函数关系式;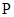 元,试写出
元,试写出 元?
元? 的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).