题目内容
已知：二次函数
的图象开口向上，并且经过原点
.
（1）求
的值；
（2）用配方法求出这个二次函数图象的顶点坐标.
（1）1；（2）（
，-
）．
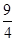解析试题分析：（1）根据二次函数图象开口向上判断出a＞0，再把原点坐标代入函数解析式求解即可；
（2）根据配方法的操作整理成顶点式解析式，然后写出顶点坐标即可．
试题解析:（1）∵图象开口向上，
∴a＞0，
∵函数图象经过原点O（0，0），
∴a2-1=0，
解得a1=1，a2=-1（舍去），
∴a=1；
（2）y=x2-3x
=x2-3x+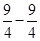
=（x-）2-，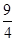
故抛物线顶点坐标为（，-）．
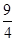考点: 1.二次函数的性质；2.二次函数的三种形式．
练习册系列答案
相关题目
某批发商以每件50元的价格购进400件T恤．若以单价70元销售,预计可售出200件．批发商的销售策略是：第一个月为增加销售量,降价销售,经过市场调查,单价每降低0.5元,可多售出5件,但最低单价不低于购进的价格;第一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元．设第一个月单价降低x元．
（1）根据题意,完成下表：
| | 每件T恤的利润（元） | 销售量（件） |
| 第一个月 | | |
| 清仓时 | | |
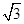）为圆心，以2为半径的圆与
轴交于A、B两点．
的图象经过点A、B，试确定此二次函数的解析式．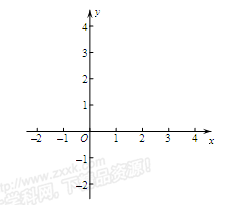
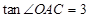，求抛物线的表达式；
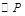相离、相切、相交.