题目内容
如图,抛物线 的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
(1)求抛物线的解析式;
(2)判断△ABC的形状,说出△ABC外接圆的圆心位置,并求出圆心的坐标.
(1)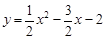 ;(2)该外接圆的圆心为AB的中点,且坐标为:
;(2)该外接圆的圆心为AB的中点,且坐标为: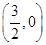 .
.
解析试题分析:(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可求解;
(2)首先根据抛物线的解析式确定A点、B点、C点坐标,然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置,由此确定圆心坐标.
试题解析:(1)∵点B(4,0)在抛物线 的图象上,∴
的图象上,∴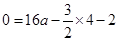 ,∴
,∴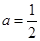 .∴抛物线的解析式为:
.∴抛物线的解析式为: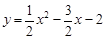 ;
;
(2)△ABC为直角三角形.令x=0,得:y=-2,∴C(0,-2),令y=0,得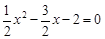 ,∴x1=-1,x2=4,∴A(-1,0),B(4,0),∴AB=5,AC=5BC=20,∴AC2+BC2=AB2,∴△ABC为直角三角形,∴AB为△ABC外接圆的直径,∴该外接圆的圆心为AB的中点,且坐标为:
,∴x1=-1,x2=4,∴A(-1,0),B(4,0),∴AB=5,AC=5BC=20,∴AC2+BC2=AB2,∴△ABC为直角三角形,∴AB为△ABC外接圆的直径,∴该外接圆的圆心为AB的中点,且坐标为: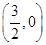 .
.
考点: ①待定系数法求二次函数解析式;②勾股定理逆定理;③三角形的外心

练习册系列答案
相关题目
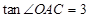 ,求抛物线的表达式;
,求抛物线的表达式; 相离、相切、相交.
相离、相切、相交.
 与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
 经过点A(0,3),B(3,0),C(4,3).
经过点A(0,3),B(3,0),C(4,3).