题目内容
如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为xm,窗户的透光面积为ym2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.
(1)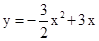 (0<x<2); (2)当窗框的长为
(0<x<2); (2)当窗框的长为 m和宽为1 m时,才能使得窗户的透光面积最大,此时的最大面积为
m和宽为1 m时,才能使得窗户的透光面积最大,此时的最大面积为 m2.
m2.
解析试题分析:(1)由窗框的宽为x m,则长为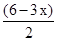 m,从而根据矩形面积公式得出函数关系式即可;
m,从而根据矩形面积公式得出函数关系式即可;
(2)根据二次函数解析式,用配方法求其最大值即可.
试题解析:(1)根据题意,得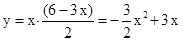 (0<x<2).
(0<x<2).
(2)∵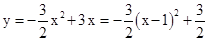 ,∴当x=1时,
,∴当x=1时, .
.
∴当窗框的长为 m和宽为1 m时,才能使得窗户的透光面积最大,此时的最大面积为
m和宽为1 m时,才能使得窗户的透光面积最大,此时的最大面积为 m2.
m2.
考点:二次函数的应用.

练习册系列答案
相关题目
某批发商以每件50元的价格购进400件T恤.若以单价70元销售,预计可售出200件.批发商的销售策略是:第一个月为增加销售量,降价销售,经过市场调查,单价每降低0.5元,可多售出5件,但最低单价不低于购进的价格;第一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元.设第一个月单价降低x元.
(1)根据题意,完成下表:
| | 每件T恤的利润(元) | 销售量(件) |
| 第一个月 | | |
| 清仓时 | | |
 中,函数y与自变量x的部分对应值如下表:
中,函数y与自变量x的部分对应值如下表: ?
? 

 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题:
 的两个根.
的两个根.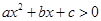 的解集.
的解集. 随
随 的增大而减小的自变量
的增大而减小的自变量 有两个不相等的实数根,求
有两个不相等的实数根,求 的取值范围.
的取值范围.
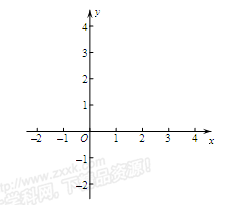
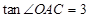 ,求抛物线的表达式;
,求抛物线的表达式;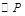 相离、相切、相交.
相离、相切、相交.