��Ŀ����
����Ŀ�����κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ��ʾ��ͼ����㣨-1��0�����Գ���Ϊֱ��x=2�����н��ۣ���1��4a+b=0����2��9a+c��3b����3��8a+7b+2c��0����4������A��-3��y1������B��-![]() ��y2������C��
��y2������C��![]() ��y3���ڸú���ͼ���ϣ���y1��y3��y2����5��������a��x+1����x-5��=-3������Ϊx1��x2����x1��x2����x1��-1��5��x2��������ȷ�Ľ����У�������
��y3���ڸú���ͼ���ϣ���y1��y3��y2����5��������a��x+1����x-5��=-3������Ϊx1��x2����x1��x2����x1��-1��5��x2��������ȷ�Ľ����У�������
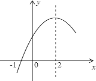
A.2��B.3��C.4��D.5��
���𰸡�B
��������
��1����ȷ�����ݶԳ��ṫʽ���㼴�ɣ�
��2����������x����3ʱ��y��0�������жϣ�
��3����ȷ����ͼ���֪�����߾�������1��0���ͣ�5��0�����г����������a��b�����жϣ�
��4���������ú���ͼ���жϣ�
��5����ȷ�����ö��κ�������β���ʽ��ϵ���ɽ�����⣮
�⣺��1����ȷ���ߩ�![]() ��2��
��2��
��4a+b��0������ȷ��
��2������x����3ʱ��y��0��
��9a��3b+c��0��
��9a+c��3b���ʣ�2������
��3����ȷ����ͼ���֪�����߾�������1��0���ͣ�5��0����
��![]() ���
���![]() ��
��
��8a+7b+2c��8a��28a��10a����30a��
��a��0��
��8a+7b+2c��0���ʣ�3����ȷ��
��4�����ߵ�A����3��y1������B����![]() ��y2������C��
��y2������C��![]() ��y3����
��y3����
��![]() ��2��
��2��![]() ��2������
��2������![]() ����
����![]() ��
��
��![]() ��
��![]()
���C��Գ���ľ������
��y3��y2��
��a��0����3����![]() ��2��
��2��
��y1��y2
��y1��y2��y3���ʣ�4������
��5����ȷ����a��0��
�ࣨx+1����x��5����![]() ��0��
��0��
����x+1����x��5����0��
��x����1��x��5���ʣ�5����ȷ��
����ȷ����������
��ѡ��B��

 ��У����ϵ�д�
��У����ϵ�д�