Question

【题目】四边形ABCD的两条对角线AC、BD互相平分．添加下列条件，一定能判定四边形ABCD为菱形的是（　　）

A.∠ABD＝∠BDCB.∠ABD＝∠BACC.∠ABD＝∠CBDD.∠ABD＝∠BCA

Answer 1

【答案】C

【解析】

先由对角线AC、BD互相平分得出四边形ABCD是平行四边形，再按照平行四边形基础上菱形的判定方法：①一组邻边相等的平行四边形是菱形；②对角线互相垂直的平行四边形是菱形，逐个选项分析即可．

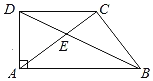
解：如图所示，设四边形ABCD的两条对角线AC、BD交于点O，

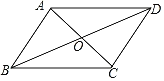
∵AC、BD互相平分，

∴四边形ABCD是平行四边形．

选项A，由平行四边形的性质可知AB∥DC，则∠ABD＝∠BDC，从而A不符合题意；

选项B，∠ABD＝∠BAC，则AO＝BO，再结合对角线AC、BD互相平分，可知AC＝BD，从而平行四边形ABCD是矩形，故B不符合题意；

选项C，由平行四边形的性质可知AD∥BC，从而∠ADB＝∠CBD，

当∠ABD＝∠CBD时，∠ADB＝∠ABD，故AB＝AD，

由一组邻边相等的平行四边形的菱形可知，C符合题意；

选项D，∠ABD＝∠BCA，得不出可以判定四边形ABCD为菱形的条件，故D不符合题意．

综上，只有选项C一定能判定四边形ABCD为菱形．

故选：C．