题目内容
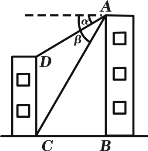
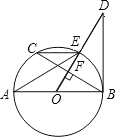
【题目】如图,AB是⊙O的直径,C为⊙O上一点,作CE⊥AB干点E,BE=2OE,延长AB至点D,使得BD=AB,P是弧AB(异于A,B)上一个动点,连接AC、PE.
(1)若AO=3,求AC的长度;
(2)求证:CD是⊙O的切线;
(3)点P在运动的过程中是否存在常数k,使得PE=k·PD,如果存在,求k的值,如果不存在,请说明理由.
【答案】(1)![]() ;(2)见解析;(3)存在,
;(2)见解析;(3)存在,![]()
【解析】
(1)AO=3,即半径为3,所以AB=6,可算出AE=4,AB是直径,且AE⊥EC,易证明△AEC∽△CEB,则有![]() ,即可算出AC长.
,即可算出AC长.
(2)连接OC,由△AEC∽△CEB,可得![]() =
=![]() ,再证明
,再证明![]() =
=![]() ,又∠OEC=∠CED可证明△OEC∽△CED,所以∠ECD=∠EOC,所以∠OCE+∠ECD=∠OCE+∠COE=
,又∠OEC=∠CED可证明△OEC∽△CED,所以∠ECD=∠EOC,所以∠OCE+∠ECD=∠OCE+∠COE=![]() ,即可证明CD为切线.
,即可证明CD为切线.
(3)连接OP,由![]() ,且∠POE=∠DOP,所以△OEP∽△OPD,即可证明
,且∠POE=∠DOP,所以△OEP∽△OPD,即可证明![]() .
.
解:(1)∵AO=3,
∴OB=3,AB=BD=6,AE=4
∵BE=2OE
∴OE=1,BE=2
∵AB是直径
∴∠ACB=![]()
∵∠AEC=![]()
∴∠CAB=∠BCE
∴△AEC∽△CEB
∴![]() =24
=24
∴AC=2![]()
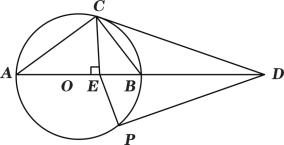
(2)如下图,连接OC,
由(1)中△AEC∽△CEB,
可得![]() =
=![]() ,EC=
,EC=![]() OE
OE
ED=EB+BD=2OE+6OE=8OE
∴![]() =
=![]() ,
,
∵∠OEC=∠CED
∴△OEC∽△CED
∴∠ECD=∠EOC,
∴∠OCE+∠ECD=∠OCE+∠COE=![]()
∴OC⊥CD,
即CD为⊙O的切线.
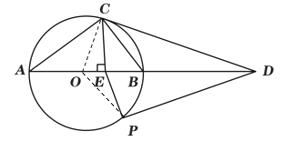
(3)存在,![]() ,如下图,连接OP
,如下图,连接OP
∴OP=OB=3OE
∵OD=9OE
∴![]()
又∵∠EOP=∠POD
∴△OEP∽△OPD
∴![]()
∴k=![]() .
.

练习册系列答案
相关题目