题目内容
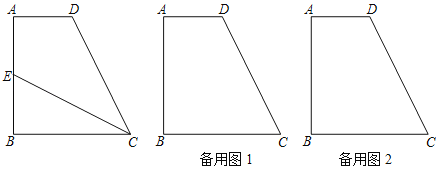
【题目】如果一条直线把一个四边形分成两部分,这两部分图形的周长相等,那么这条直线称为这个四边形的“等分周长线”.在直角梯形ABCD中,AB∥CD,∠A=90°,DC=AD,∠B是锐角,cotB=![]() ,AB=17.如果点E在梯形的边上,CE是梯形ABCD的“等分周长线”,那么△BCE的周长为____.
,AB=17.如果点E在梯形的边上,CE是梯形ABCD的“等分周长线”,那么△BCE的周长为____.
【答案】42
【解析】
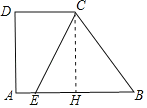
作CH⊥AB于H,设BH=5a,证明四边形ADCH为矩形,得到AD=CH=12a,根据题意求出a,根据勾股定理求出BC,根据“等分周长线”计算,得到答案.
解:作CH⊥AB于H,
设BH=5a,
∵cotB=![]() ,
,
∴![]() =
=![]() ,
,
∴CH=12a,
∵AB∥CD,
∴∠D=∠A=90°,又CH⊥AB,
∴四边形ADCH为矩形,
∴AD=CH=12a,CD=AH,
∵DC=AD,
∴AH=CD=12a,
由题意得,12a+5a=17,
解得,a=1,
∴AD=CD=AH=12,BH=5,
在Rt△CHB中,BC=![]() =13,
=13,
∴四边形ABCD的周长=12+12+17+13=54,
∵CE是梯形ABCD的“等分周长线”,
∴点E在AB上,
∴AE=17+13﹣27=3,
∴EH=12﹣3=9,
由勾股定理得,EC=![]() =15,
=15,
∴△BCE的周长=14+13+15=42,
故答案为:42.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目