Question

【题目】如图示，AB是⊙O的直径，点F是半圆上的一动点（F不与A，B重合），弦AD平分∠BAF，过点D作DE⊥AF交射线AF于点AF．

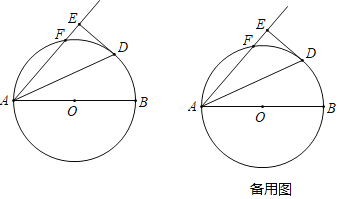
（1）求证：DE与⊙O相切：

（2）若AE＝8，AB＝10，求DE长；

（3）若AB＝10，AF长记为x，EF长记为y，求y与x之间的函数关系式，并求出AFEF的最大值．

Answer 1

【答案】（1）见解析；（2）4；（3）y＝﹣x+5，

【解析】

（1）连接OD，根据三角形外角和，AD是∠BAF的角平分线求得OD∥AF，又由DE⊥AF，即可得到DE与⊙O相切；

（2）连接BD，先找出△AED∽△ADB，根据AD：AB＝AE：AD求出AD2＝80，在Rt△AED中，根据勾股定理求解即可；

（3）连接DF，过点D作DG⊥AB于G，证明△AED≌△AGD，得到∠FAD＝∠DAB，进而得到即DF＝DB，在求证Rt△DEF≌Rt△DGB，得到AB=AF+2EF，即x+2y=10，得到AEEF＝﹣x2+5x，求该二次函数最大值即可．

（1）证明：连接OD，如图1所示：

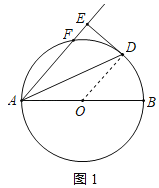
∵OD＝OA，

∴∠OAD＝∠ODA，

∵AD平分∠BAF，

∴∠OAD＝∠FAD，

∴∠ODA＝∠FAD，

∴OD∥AF，

∵DE⊥AF，

∴DE⊥OD，

又∵OD是⊙O的半径，

∴DE与⊙O相切；

（2）解：连接BD，如图2所示：

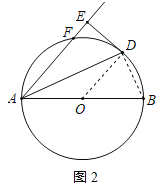
∵AB是⊙O的直径，

∴∠ADB＝90°，

∵DE⊥AF，

∴∠AED＝90°＝∠ADB，

又∵∠EAD＝∠DAB，

∴△AED∽△ADB，

∴AD：AB＝AE：AD，

∴AD2＝AB×AE＝10×8＝80，

在Rt△AED中，由勾股定理得：DE＝ ＝＝4；

（3）连接DF，过点D作DG⊥AB于G，如图3所示：

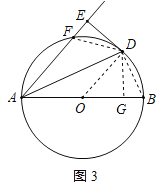
在△AED和△AGD中，，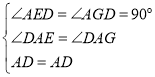

∴△AED≌△AGD（AAS），

∴AE＝AG，DE＝DG，

∵∠FAD＝∠DAB，

∴，

∴DF＝DB，

在Rt△DEF和Rt△DGB中，，

∴Rt△DEF≌Rt△DGB（HL），

∴EF＝BG，

∴AB＝AG+BG＝AF+EF＝AF+EF+EF＝AF+2EF，

即：x+2y＝10，

∴y＝﹣x+5，

∴AEEF＝﹣x2+5x＝﹣（x﹣5）2+，

∴AFEF有最大值，当x＝5时，AFEF的最大值为．