题目内容
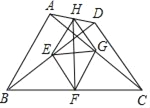
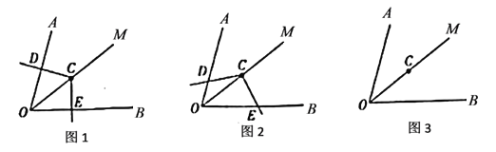
【题目】已知：如图
，
是
的平分线，点
在上，
，且点到
的距离为
，过点作
，
，垂足分别为
，
，易得到结论：
．
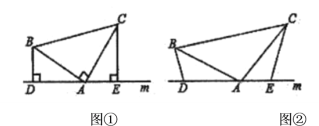
（1）把图中的
绕点旋转，当
与不垂直时（如图
），上述结论是否成立？并说明理由．
（2）把图中的绕点旋转，当与的反向延长线相交于点时：
①请在图中画出图形；
②上述结论还成立吗？若成立，请给出证明；若不成立，请直接写出线段
，
之间的的数量关系，不需证明．
【答案】8;（1）成立，理由见解析；（2）①见解析，②不成立，
【解析】
先根据角平分线的性质得出
，然后根据
得出
，利用勾股定理即可求出OD的值，然后即可求出
的值；
（1）过点
作
，
分别交
，
于点
，
，则
，首先证明
，得出
，然后利用勾股定理求出
的值，再证明
，得出
，最后通过等量代换即可求出的值；
（2）①根据题意画出图形即可；
②过点作
，
交，于点
，
，按照（1）的方法可得
，
，得出
，
，
然后通过等量代换得出．
∵
是
的平分线， 
，
在
和
中，
（1）成立．理由：
过点作，分别交，于点，，则，
是的平分线，，
，
，
在
和
中，
，
，点到的距离为
，即
，
根据题意得，
，
在
和
中，
，
，
（2）①所作图形如图所示
②不成立，
过点作，交，于点，，
是的平分线，，
，
，
在
和
中，
，
，点到的距离为，即
，
根据题意得，
，
在
和
中，
，
，
，
，
∴
练习册系列答案
名校课堂系列答案
相关题目
