题目内容
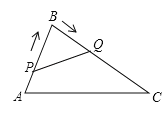
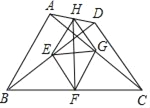
【题目】如图,E,F,G,H分别是BD,BC,AC,AD的中点,且AB=CD,下列结论:①EG⊥FH;②四边形EFGH是菱形;③HF平分∠EHG;④EG=![]() (BC﹣AD),其中正确的个数是( )
(BC﹣AD),其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
根据三角形的中位线平行于第三边并且等于第三边的一半与AB=CD可得四边形EFGH是菱形;
然后根据菱形的对角线互相垂直平分,并且平分每一组对角的性质对各小题进行判断,从而找出正确的个数即可得到答案.
∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴EF=![]() CD,FG=
CD,FG=![]() AB,GH=
AB,GH=![]() CD,HE=
CD,HE=![]() AB,
AB,
∵AB=CD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形,
∴①EG⊥FH,正确;
②四边形EFGH是菱形,正确;
③HF平分∠EHG,正确;
④当AD∥BC,如图所示:E,G分别为BD,AC中点,
∴连接CD,延长EG到CD上一点N,
如下图所示:
![]()
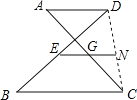
∴EN=![]() BC,GN=
BC,GN=![]() AD,
AD,
∴EG=![]() (BC-AD),只有AD∥BC时才可以成立,而本题AD与BC很显然不平行,故本小题错误;
(BC-AD),只有AD∥BC时才可以成立,而本题AD与BC很显然不平行,故本小题错误;
故①②③对.
故选C.

练习册系列答案
相关题目