Question

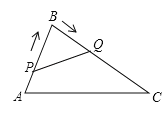
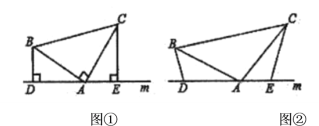
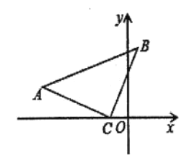
【题目】问题背景：（1）如图，已知中，，直线经过点直线，直线，垂足分别为点．求证：．

证明：

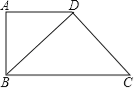
拓展延伸：（2）如图，将（1）中的条件改为：在中，三点都在直线上，并且有．请写出三条线段的数量关系．（不需要证明）

实际应用：（3）如图，在中，，点的坐标为，点的坐标为，请直接写出点的坐标．

Answer 1

【答案】（1）见解析；（2）DE＝BD＋CE；（3）B（1，4）.

【解析】

（1）根据BD⊥直线m，CE⊥直线m得∠BDA=∠CEA=90°，而∠BAC=90°，根据等角的余角相等得∠CAE=∠ABD，然后根据“AAS”可判断△ADB≌△CEA，则AE=BD，AD=CE，于是DE=AE+AD=BD+CE；（2）利用∠BDA=∠BAC，得出∠CAE=∠ABD，进而得出△ADB≌△CEA即可得出答案．（3）过点A、B分别作x轴的垂线，垂足分别为D、E，构造（1）中的模型，进而利用（1）的结论即可求解.

(1) 证明：∵BD⊥直线m，CE⊥直线m，

∴∠BDA＝∠CEA＝90°，

∵∠BAC＝90°，

∴∠BAD＋∠CAE＝90°，

∵∠BAD＋∠ABD＝90°，

∴∠CAE＝∠ABD，

在△ADB和△CEA中，

∵，

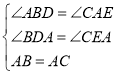∴△ADB≌△CEA(AAS)，

∴AE＝BD，AD＝CE，

∴DE＝AE＋AD＝BD＋CE；

(2) DE＝BD＋CE.理由如下：

∵∠BDA＝∠BAC＝∠AEC，

∴∠DBA＋∠BAD＝∠BAD＋∠CAE，

∴∠CAE＝∠ABD，

在△ADB和△CEA中，

∵，

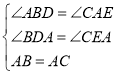∴△ADB≌△CEA(AAS)，

∴AE＝BD，AD＝CE，

∴DE＝AE＋AD＝BD＋CE；

（3）如图，过点A、B分别作x轴的垂线，垂足分别为D、E，

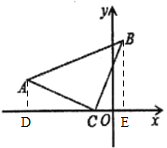
由（1）可知，AD=CE，CD=BE，

∵点的坐标为，点的坐标为，

∴AD=3，CD=4，

∴OE=1，

∴点B的坐标为（1，4）.