题目内容
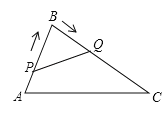
【题目】如图,在△ABC中,∠B=60°,过点C作CD∥AB,若∠ACD=60°,求证:△ABC是等边三角形.

【答案】见解析.
【解析】
证法一:根据平行线的性质可知,∠A=60°,所以∠ACB=60°,即可证明△ABC是等边三角形.
证法二:根据平行线的性质可知,∠B=60°,所以∠BCD=120°,∠ACB=60°,即可证明△ABC是等边三角形.
证明:
证法一: ∵ CD∥AB,
∴ ∠A=∠ACD=60°.
∵ ∠B=60°,
在△ABC中,
∠ACB=180°-∠A-∠B=60°.
∴ ∠A=∠B=∠ACB.
∴ △ABC是等边三角形.
证法二: ∵ CD∥AB,
∴ ∠B+∠BCD=180°.
∵ ∠B=60°,
∴ ∠BCD=120°.
∴ ∠ACB=∠BCD-∠ACB=60°.
在△ABC中,
∠A=180°-∠B-∠ACB=60°.
∴ ∠A=∠B=∠ACB.
∴ △ABC是等边三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目