题目内容
【题目】如图，
，
为五边形
的对角线，
，
，
，
，
，若四边形
的面积为36，则
__________．
【答案】
【解析】
过点D作
于点H，过点E作
于点G，连接BE,取BE的中点O，连接OD,OC，先利用全等三角形的性质和角平分线的定义得出
，然后利用角度之间的计算和直角三角形的性质，三角形外角的性质得出
为等边三角形，进而得出
，然后接着证明四边形AHGE是矩形，得出
，设
利用四边形ABCE面积和HD的长度得到两个关于x,y的方程，联立即可解出x,y的值，然后求出
，最后利用即可求BC的长度．
过点D作于点H，过点E作于点G，连接BE,取BE的中点O，连接OD,OC
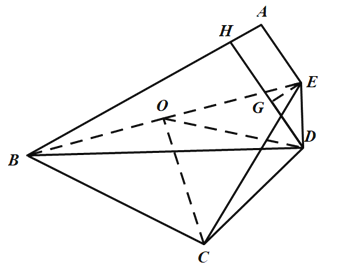
在
和
中，
,
为等边三角形
∵， ，
∴四边形AHGE是矩形，
设
则四边形ABCE的面积为
∴
又
∵
解得
解得
故答案为：．
练习册系列答案
相关题目
【题目】某日王老师佩戴运动手环进行快走锻炼，两次锻炼后数据如表．与第一次锻炼相比，王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍．设王老师第二次锻炼时平均步长减少的百分率为
．
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) | 10000 | ____________ |
平均步长(米/步) | 0.6 | ____________ |
距离(米) | 6000 | 7020 |
注：步数×平均步长＝距离．
(1)根据题意完成表格填空；
(2)求x；
(3)王老师发现好友中步数排名第一为24000步，因此在两次锻炼结束后又走了500米，使得总步数恰好为24000步，求王老师这500米的平均步长．
