题目内容
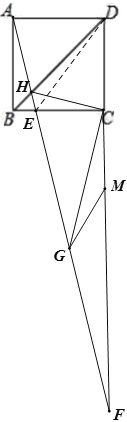
【题目】已知正方形ABCD,点F是射线DC上一动点(不与C,D重合).连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G.
(1)若点F在边CD上,如图1.
①证明:∠DAH=∠DCH;
②猜想:△GFC的形状并说明理由.
(2)取DF中点M,连接MG.若MG=2.5,正方形边长为4,求BE的长.

【答案】(1)①证明见解析;②△GFC是等腰三角形,理由见解析;(2)BE的长为1或7.
【解析】
(1)①根据正方形的性质可得AD=CD,∠ADH=∠CDH,利用SAS可证明△ADH≌△CDH,即可得∠DAH=∠DCH;
②由正方形的性质可得∠DAH+∠AFD=90°,由CG⊥HC可得∠DCH+∠FCG=90°,根据∠AFD=∠CFG,可得∠CFG=∠FCG,即可证明CG=FG,可得△GFC是等腰三角形;
(2)当点F在线段CD上时,连接DE,根据正方形的性质及角的和差关系可得∠E=∠GCE,即可证明CG=EG,由△GFC是等腰三角形可得CG=GF,可得点G为EF中点,即可证明GM是△FDE的中位线,根据中位线的性质可求出DE的长,利用勾股定理可求出CE的长,进而根据BE=BC+CE即可求出BE的长;当点F在DC延长线上时,连接DE,同理可得MG为△FDE的中位线,可求出DE的长,利用勾股定理可求出CE的长,根据BE=BC-CE即可求出BE的长.
(1)①∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ADB=∠CDB=45°,
在△ADH和△CDH中,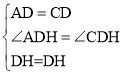 ,
,
∴△ADH≌△CDH,
∴∠DAH=∠DCH.
②△GFC是等腰三角形,理由如下:
∵四边形ABCD是正方形,CG⊥HC,
∴∠ADF=∠HCG=90°,
∴∠DAH+∠AFD=DCH+∠DCG=90°,
∵∠DAH=∠DCH,∠HFD=∠CFG,
∴∠CFG=∠GCF,
∴CF=CG,
∴△GFC是等腰三角形.
(2)如图,当点F在线段CD上时,连接DE,
∵四边形ABCD是正方形,
∴∠CEF+∠CFG=90°,∠GCE+∠GCF=90°,
∵∠CFG=∠GCF,
∴∠CEF=∠GCE,
∴CG=EG,
∵CG=FG,
∴FG=EG,
∵点M是DF的中点,
∴GM是△DFE的中位线,
∵GM=2.5,
∴DE=2GM=5,
∵正方形ABCD的边长为4,
∴CE=![]() =3,
=3,
∴BE=BC+CE=4+3=7.
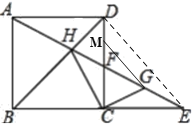
如图,当点F在DC的延长线上时,连接DE,
同理可得:MG为△DFE的中位线,
∴DE=2GM=5,
∴CE=![]() =3,
=3,
∴BE=BC-CE=4-3=1,
综上所述:BE的长为1或7.