题目内容
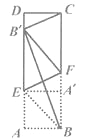
【题目】如图,将矩形纸片ABCD折叠,使点A与BC边上的点A′重合,折痕为BE,再沿过点E的直线折叠,使点B与AD边上的点 B重合,折痕为EF,连结![]() ,
,![]() .
.![]() ,则
,则![]() 的值为________
的值为________
【答案】![]()
【解析】根据矩形纸片ABCD折叠,使点A与BC边上的点 A ′ 重合,折痕为BE,可证得四边形ABA′ E是正方形,设AB=x,则BE=![]() x,再根据再沿过点E的直线折叠,使点B与AD边上的点 B ′ 重合,折痕为EF,证得易证四边形B′EBF是菱形,求出B′E、A′F的长,然后证明△CB′D≌△EFA′,可证得DB′=A′F,根据AD=AE+B′E+B′D,可得出结果.
x,再根据再沿过点E的直线折叠,使点B与AD边上的点 B ′ 重合,折痕为EF,证得易证四边形B′EBF是菱形,求出B′E、A′F的长,然后证明△CB′D≌△EFA′,可证得DB′=A′F,根据AD=AE+B′E+B′D,可得出结果.
如图,设EF与BB交于点O

∵矩形纸片ABCD折叠,使点A与BC边上的点 A ′ 重合,折痕为BE
∴AB=AB,∠A=∠ABA′ ,∠EA′ B=90°
∴四边形ABA′ E是正方形,
设AB=x,则BE=![]() x
x
∵再沿过点E的直线折叠,使点B与AD边上的点 B ′ 重合,折痕为EF
∴易证四边形B′EBF是菱形,
∴BF=BE=B′E=![]() x,B′ B⊥EF,
x,B′ B⊥EF,
∴∠BB′ F=∠FBB′ ,∠FOB=90°
∵∠DCB′ =∠BB′ F
∴∠DCB′ =∠FBB′
∵∠1+∠FEA′=90°,∠1+FBO=90°
∴∠FEA′=∠FBO=∠DCB′
在△CB′D和△EFA′中

∴△CB′D≌△EFA′(ASA)
∴DB′=A′F
∴A′F=BF-BA′=![]() x-x
x-x
∴AD=AE+B′E+B′D=x+![]() x+
x+![]() x-x=2
x-x=2![]() x
x
∴![]()
故答案为:2![]() .
.

练习册系列答案
相关题目






