Question

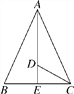
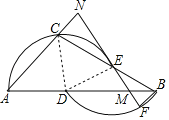
【题目】如图，已知D，E分别为△ABC的边AB，BC上两点，点A，C，E在⊙D上，点B，D在⊙E上．F为上一点，连接FE并延长交AC的延长线于点N，交AB于点M．

（1）若∠EBD为α，请将∠CAD用含α的代数式表示；

（2）若EM=MB，请说明当∠CAD为多少度时，直线EF为⊙D的切线；

（3）在（2）的条件下，若AD=，求的值．

Answer 1

【答案】（1）；（2）45°；（3）2+

【解析】

（1）根据同圆的半径相等和等边对等角得：∠EDB=∠EBD=α，∠CAD=∠ACD，∠DCE=∠DEC=2α，再根据三角形内角和定理可得结论；

（2）设∠MBE=x，同理得：∠EMB=∠MBE=x，根据切线的性质知：∠DEF=90°，所以∠CED+∠MEB=90°，同理根据三角形内角和定理可得∠CAD=45°；

（3）由（2）得：∠CAD=45°；根据（1）的结论计算∠MBE=30°，证明△CDE是等边三角形，得CD=CE=DE=EF=AD=，求EM=1，MF=EF﹣EM=﹣1，根据三角形内角和及等腰三角形的判定得：EN=CE=，代入化简可得结论．

（1）连接CD、DE，

在⊙E中，∵ED=EB，

∴∠EDB=∠EBD=α，

∴∠CED=∠EDB+∠EBD=2α，

在⊙D中，∵DC=DE=AD，

∴∠CAD=∠ACD，∠DCE=∠DEC=2α，

△ACB中，∠CAD+∠ACD+∠DCE+∠EBD=180°，

∴∠CAD==；

（2）设∠MBE=x，

∵EM=MB，

∴∠EMB=∠MBE=x，

当EF为⊙D的切线时，∠DEF=90°，

∴∠CED+∠MEB=90°，

∴∠CED=∠DCE=90°﹣x，

△ACB中，同理得，∠CAD+∠ACD+∠DCE+∠EBD=180°，

∴2∠CAD=180°﹣90∴=90∴，

∴∠CAD=45°；

（3）由（2）得：∠CAD=45°；

由（1）得：∠CAD=；

∴∠MBE=30°，

∴∠CED=2∠MBE=60°，

∵CD=DE，

∴△CDE是等边三角形，

∴CD=CE=DE=EF=AD=，

Rt△DEM中，∠EDM=30°，DE=，

∴EM=1，MF=EF﹣EM=﹣1，

△ACB中，∠NCB=45°+30°=75°，

△CNE中，∠CEN=∠BEF=30°，

∴∠CNE=75°，

∴∠CNE=∠NCB=75°，

∴EN=CE=，

∴===2+．