题目内容
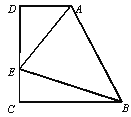
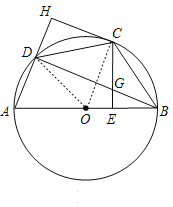
【题目】如图,四边形ABCD内接于⊙O,AB为直径,BC=CD,过点C作CE⊥AB于点E,CH⊥AD交AD的延长线于点H,连接BD交CE于点G.
(1)求证:CH是⊙O的切线;
(2)若点D为AH的中点,求证:AD=BE;
(3)若sin∠DBA=![]() ,CG=5,求BD的长.
,CG=5,求BD的长.

【答案】(1)见解析;(2)见解析;(3)16
【解析】
(1)连接OC,OD,证得∠BAH=∠BOC,得出AH∥OC,则OC⊥CH,则结论得证;
(2)连接AC,得出CE=CH,证明Rt△CEB≌Rt△CHD(HL),则BE=DH,证出AD=DH,则可得出结论;
(3)延长CE交⊙O于点F,得出GB=GC=5,在Rt△GEB中,sin∠GBE=![]() ,可求出GE=3,由勾股定理求出BE,证明Rt△AEC∽△Rt△CEB,由
,可求出GE=3,由勾股定理求出BE,证明Rt△AEC∽△Rt△CEB,由![]() 可求出AE,再求出AD,则可得出BD的长.
可求出AE,再求出AD,则可得出BD的长.
(1)证明:如图,连接OC,OD,
∵BC=CD,
∴∠BOC=∠COD=![]() ∠BOD,
∠BOD,
又∵∠BAH=![]() ∠BOD,
∠BOD,
∴∠BAH=∠BOC,
∴AH∥OC,
∵AH⊥CH,
∴OC⊥CH,
∴CH是⊙O的切线;
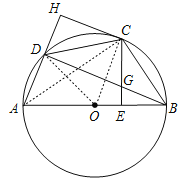
(2)证明:如图,连接AC,
∵BC=CD,
∴![]() ,
,
∴∠BAC=∠CAH,
又∵CE⊥AB,CH⊥AH,
∴CE=CH,
∴Rt△CEB≌Rt△CHD(HL),
∴BE=DH,
∵点D为AH的中点,
∴AD=DH,
∴AD=BE;
(3)解:如图,延长CE交⊙O于点F,
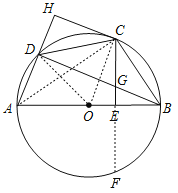
∵AB是⊙O的直径,CF⊥AB,
∴![]() =
=![]() =
=![]() ,
,
∴∠BCE=∠CBD,
∴GB=GC=5,
在Rt△GEB中,sin∠GBE=![]() ,
,
∴GE=3,
∴BE=![]() =
=![]() =4,
=4,
CE=CG+GE=5+3=8,
∵∠EAC=∠CAD=∠CBD=∠BCE,∠AEC=∠CEB=90°,
∴Rt△AEC∽△Rt△CEB,
∴![]() ,
,
即![]() ,
,
∴AE=16,
∴AB=AE+BE=16+4=20,
在Rt△ADB中,sin∠DBA=![]() ,
,
∴AD=![]() AB=
AB=![]() ×20=12,
×20=12,
∴BD=![]() =
=![]() =16.
=16.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案