Question

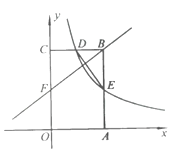
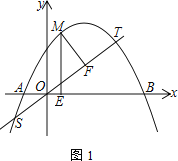
【题目】若抛物线上，它与轴交于，与轴交于、，是抛物线上、之间的一点，

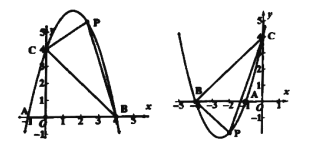
（1）当时，求抛物线的方程，并求出当面积最大时的的横坐标。

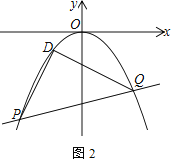
（2）当时，求抛物线的方程及的坐标，并求当面积最大时的横坐标。

（3）根据（1）、（2）推断的横坐标与的横坐标有何关系？

Answer 1

【答案】（1）2；（2）－2；（3）的横坐标等于的横坐标的一半

【解析】

（1）将k=4代入化成交点式，然后将C（0,4）代入确定a的值，求得B点坐标，连接OP；设，即可求出△BCP的面积表达式，然后求最值即可.

（2）设，将代入得，得到二次函数解析式；令y=0，求出直线BC所在的直线方程；过作平行于轴，交直线于，设、，求出△BCP的面积表达式，然后求最值即可.

（3）由（1）（2）的解答过程，进行推断即可.

解：（1）时，

由交点式得，

代入得，

∴，

∵k=4

∴B点坐标;

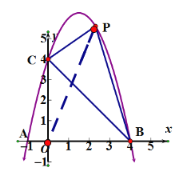
连，设，

时，最大值为8，

∴的横坐标为2时有最大值.

（2）当时，，

设，

代入得，

∴.

令求得，

易求直线方程为，

过作平行于轴交直线于，

设、，

面积最大值为8，

此时P的横坐标为-2.

（3）根据（1）（2）得，面积最大时的横坐标等于的横坐标的一半.