题目内容
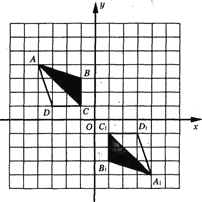
【题目】如图，在网格中、建立了平面直角坐标系，每个小正方形的边长均为1个单位长度，将四边形ABCD 绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1．
(1)直接写出点D1的坐标________，点D旋转到点D1所经过的路线长_______；
(2)请你在△ACD的三个内角中任选一个锐角，若你所选的锐角是________，则它所对应的正弦函数值是_________；
(3)将四边形A1B1C1D1平移，得到四边形A2B2C2D2，若点D2（4，5），画出平移后的图形．
【答案】(3，－1) 
∠ACD 
【解析】
解：（1）如图：点D的坐标为（-3，1），
∵将四边形ABCD绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1
∴点D1的坐标为：（3，-l），
由勾股定理得：OD=
∴点D旋转到点D1所经过的路线长=
π；
（2）∠ACD，
(或∠DAC，
)（3）正确图形如图所示：
练习册系列答案
相关题目
