题目内容
19. 如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+$\frac{12}{5}$与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M.
如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+$\frac{12}{5}$与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M.(1)求点A,B的坐标;
(2)求OM的长;
(3)存在直线l上的点P,y轴上的点Q,使得以O,P,Q为顶点的三角形与△OMP全等,请求出所有符合条件的点Q的坐标.
分析 (1)利用坐标轴上,点的坐标的特点即可得出点A,B坐标;
(2)利用三角形的面积公式建立方程即可得出OM,
(3)先判断出满足条件的两个三角形全等,只有∠OQP=90°,再分PQ=OM和OQ=OM两种情况讨论计算.
解答 解:(1)令x=0,
∴y=$\frac{12}{5}$,
∴B(0,$\frac{12}{5}$);
令y=0,
∴-$\frac{3}{4}$x+$\frac{12}{5}$=0,
∴x=$\frac{16}{5}$,
∴A($\frac{16}{5}$,0);
∴A($\frac{16}{5}$,0),B(0,$\frac{12}{5}$);
(2)由(1)知,A($\frac{16}{5}$,0),B(0,$\frac{12}{5}$);
∴OA=$\frac{16}{5}$,OB=$\frac{12}{5}$,AB=4,
∵OM⊥AB,
∴S△AOB=$\frac{1}{2}OA×OB$=$\frac{1}{2}$AB×OM,
∴OM=$\frac{OA×OB}{AB}$=$\frac{48}{25}$;
(3)∵以O,P,Q为顶点的三角形与△OMP全等,
∴OP是公共边,在Rt△OMP中,OP为斜边,
∴∠OQP=90°,
∴PQ∥x轴,
∵以O,P,Q为顶点的三角形与△OMP全等,
∴PQ=OM或OQ=OM,
①当PQ=OM时,
∴PQ=OM=$\frac{48}{25}$,
∴P点横坐标为$\frac{48}{25}$或-$\frac{48}{25}$,
Ⅰ、当点P横坐标为$\frac{48}{25}$,
∴点P的纵坐标为:$\frac{24}{25}$,
∴P($\frac{48}{25}$,$\frac{24}{25}$),
∴Q(0,$\frac{24}{25}$).
Ⅱ、当点P横坐标为:-$\frac{48}{25}$,
∴点P的纵坐标为:$\frac{96}{25}$,
∴P(-$\frac{48}{25}$,$\frac{96}{25}$),
∴Q(0,$\frac{96}{25}$).;
②当OQ=OM时,OQ=OM=$\frac{48}{25}$,
∴Q(0,$\frac{48}{25}$)或(0,-$\frac{48}{24}$);
即:满足条件的点Q的坐标为(0,$\frac{24}{25}$).或(0,$\frac{96}{25}$).或(0,$\frac{48}{25}$)或(0,-$\frac{48}{24}$).
点评 此题是一次函数综合题,主要考查了坐标轴上点的特征,三角形的面积公式,全等三角形的判定,解本题的关键是用方程的思想列出方程,是一道中等难度的中考常考题.

 名校课堂系列答案
名校课堂系列答案 某小区规划在一个长为40米,宽为26米的矩形场地ABCD上修建三条同样宽的甬路,使其中两条与AB平行,另一条与AB垂直,其余部分种草,若使每一块草坪的面积都为144米2,则甬路的宽度为2米.
某小区规划在一个长为40米,宽为26米的矩形场地ABCD上修建三条同样宽的甬路,使其中两条与AB平行,另一条与AB垂直,其余部分种草,若使每一块草坪的面积都为144米2,则甬路的宽度为2米.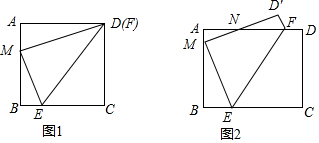
 已知两个有理数a,b在数轴上的位置如图所示:
已知两个有理数a,b在数轴上的位置如图所示: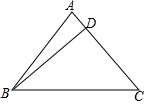 如图,△ABC中,AB=AC=5,BC=6,BD⊥AC于点D,将△BCD绕点B逆时针旋转,旋转角的大小与∠CBA相等,如果点C、D旋转后分别落在点E、F的位置,那么∠EFD的正切值是$\frac{1}{2}$.
如图,△ABC中,AB=AC=5,BC=6,BD⊥AC于点D,将△BCD绕点B逆时针旋转,旋转角的大小与∠CBA相等,如果点C、D旋转后分别落在点E、F的位置,那么∠EFD的正切值是$\frac{1}{2}$.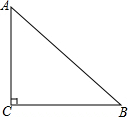 如图,已知在△ABC中,∠C=90°,AC<BC,D为BC上一点,且到A、B两点的距离相等.
如图,已知在△ABC中,∠C=90°,AC<BC,D为BC上一点,且到A、B两点的距离相等. 如图,O为△ABC内部一点,OB=3,P、R为O分别以直线AB、直线BC为对称轴的对称点.
如图,O为△ABC内部一点,OB=3,P、R为O分别以直线AB、直线BC为对称轴的对称点.