题目内容
14.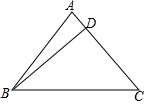 如图,△ABC中,AB=AC=5,BC=6,BD⊥AC于点D,将△BCD绕点B逆时针旋转,旋转角的大小与∠CBA相等,如果点C、D旋转后分别落在点E、F的位置,那么∠EFD的正切值是$\frac{1}{2}$.
如图,△ABC中,AB=AC=5,BC=6,BD⊥AC于点D,将△BCD绕点B逆时针旋转,旋转角的大小与∠CBA相等,如果点C、D旋转后分别落在点E、F的位置,那么∠EFD的正切值是$\frac{1}{2}$.
分析 作AH⊥BC于H,延长CD交EF于G,根据等腰三角形的性质和勾股定理求出AH、BD、CD、AD,根据旋转变换的性质得到∠FBD=∠CBA,证明FB∥AH,根据四点共圆得到∠EFD=∠GBD,求出tan∠GBD即可.
解答  解:作AH⊥BC于H,延长CD交EF于G,
解:作AH⊥BC于H,延长CD交EF于G,
∵AB=AC,
∴BH=CH=$\frac{1}{2}$BC=3,
由勾股定理得,AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=4,
$\frac{1}{2}$×BC×AH=$\frac{1}{2}$×AC×BD,即6×4=5×BD,
解得,BD=$\frac{24}{5}$,
∴CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\frac{18}{5}$,AD=$\frac{7}{5}$,
∵∠FBD=∠CBA,
∴∠FBE=∠DBC,
∵∠DBC+∠C=90°,∠HAC+∠C=90°,
∴∠FBE=∠BAH,
∴FB∥AH,
∴∠FBC=∠AHC=90°,
∴EF∥BC,
∴∠E=∠ABC=∠C=∠EGA,
∴AG=AE=BE-AB=BC-AB=1,
∴DG=$\frac{12}{5}$,
∴∠F=∠BDC=90°,
∴F、B、D、G四点共圆,
∴∠EFD=∠GBD,
tan∠GBD=$\frac{GD}{BD}$=$\frac{1}{2}$,
∴∠EFD的正切值是$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查的是旋转变换的性质、等腰三角形的性质、锐角三角函数的应用,掌握旋转变换的性质、熟记锐角三角函数的概念是解题的关键.

练习册系列答案
相关题目
6.下列各数中,是负数的是( )
| A. | $-(-\frac{1}{5})$ | B. | $-|-\frac{1}{4}|$ | C. | ${(-\frac{1}{3})^2}$ | D. | $|-\frac{1}{6}|$ |
7.点P(-3,6)关于x轴的对称点P′的坐标是( )
| A. | (3,5) | B. | (5,-3) | C. | (3,-5) | D. | (-3,-5) |
 小明将一把木匠用的直角尺和一块等腰直角三角板按如图的水平放在桌面上,且将等腰直角三角板ABC的顶点A、B分别紧靠在直角尺的内直角边DF、DE上滑动.若斜边AB=10,DF>DE≥5$\sqrt{2}$,当点B从点D滑动到点E的过程中,图中的一些边角大小发生了变化,则直角顶点C、D之间的线段CD长度的最大值为10.
小明将一把木匠用的直角尺和一块等腰直角三角板按如图的水平放在桌面上,且将等腰直角三角板ABC的顶点A、B分别紧靠在直角尺的内直角边DF、DE上滑动.若斜边AB=10,DF>DE≥5$\sqrt{2}$,当点B从点D滑动到点E的过程中,图中的一些边角大小发生了变化,则直角顶点C、D之间的线段CD长度的最大值为10. 如图,∠CAB=45°,AB=3,△ABC的面积为3,E为BC上任意一点,连AE,将△ABE,△ACE分别延AB,AC翻折至△ABM,△ACN,连MN,则MN的最小值$\frac{6}{5}$$\sqrt{10}$.
如图,∠CAB=45°,AB=3,△ABC的面积为3,E为BC上任意一点,连AE,将△ABE,△ACE分别延AB,AC翻折至△ABM,△ACN,连MN,则MN的最小值$\frac{6}{5}$$\sqrt{10}$. 如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+$\frac{12}{5}$与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M.
如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+$\frac{12}{5}$与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M.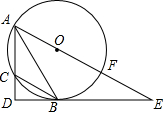 如图,已知△ABC是⊙O内接三角形,过点B作BD⊥AC于点D,连接AO并延长交⊙O于点F,交DB的延长线于点E,且点B是$\widehat{CF}$的中点.
如图,已知△ABC是⊙O内接三角形,过点B作BD⊥AC于点D,连接AO并延长交⊙O于点F,交DB的延长线于点E,且点B是$\widehat{CF}$的中点.