题目内容
10.矩形ABCD中,点E为BC上一点,BE=$\frac{1}{4}$BC,点F为边AD上的一个动点,连接EF,将矩形ABCD沿着EF翻折,使点C恰好落在AB上,其对应点为M.(1)如图1,当点F与点D重合时,求证:△AMD∽△BEM;
(2)当$\frac{DF}{AD}$=$\frac{1}{5}$时,如图2,点D的对应点为点D′,D′M与AD交于点N,求证:AN=FD.
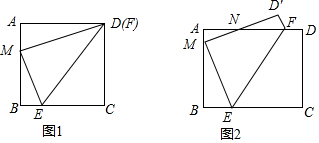
分析 (1)因为△DEM是由△DEC翻折得到,是由∠DME=∠C=90°,推出∠AMD+∠BME=90°,∠BME+∠MEB=90°,推出∠AMD=∠MEB,由此不难证明.
(2)由△D′FN∽△AMN∽△BEM,BE=$\frac{1}{4}$BC,推出EC:BE=EM:BE=3:1,推出D′F:FN=1:3,设DF=FD′=a,则FN=3a,因为DF=$\frac{1}{5}$AD,推出AD=5a,推出AN=AF-FN=4a-3a=a,由此即可证明.
解答 证明:(1)如图1中,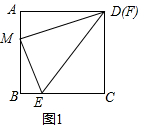
∵四边形ABCD是矩形,
∴∠A=∠C=∠B=90°,
∵△DEM是由△DEC翻折得到,
∴∠DME=∠C=90°,
∴∠AMD+∠BME=90°,∠BME+∠MEB=90°,
∴∠AMD=∠MEB,∵∠A=∠B=90°,
∴△AMD∽△BEM.
(2)如图2中,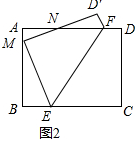
同理可证△AMN∽△BEM,
∵∠A=∠D′=90°,∠ANM=∠FND′,
∴△D′FN∽△AMN∽△BEM,
∵BE=$\frac{1}{4}$BC,
∴EC:BE=EM:BE=3:1,
∴D′F:FN=1:3,设DF=FD′=a,则FN=3a,
∵DF=$\frac{1}{5}$AD,
∴AD=5a,
∴AN=AF-FN=4a-3a=a,
∴AN=DF=a.
∴AN=DF.
点评 本题考查相似三角形的判定和性质、矩形的性质、翻折变换等知识,灵活运用相似三角形的性质是解题的关键,学会利用参数解决问题,是由中考常考题型.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
1.对于一元二次方程2x2+1=3x,下列说法错误的是( )
| A. | 二次项系数是2 | B. | 一次项系数是3 | C. | 常数项是1 | D. | x=1是它的一个根 |
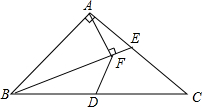 在等腰Rt△ABC中,∠BAC=90°,D为BC中点,且CE=AE,过A作AF⊥BE于F,若DF=2$\sqrt{2}$,则EF=2.
在等腰Rt△ABC中,∠BAC=90°,D为BC中点,且CE=AE,过A作AF⊥BE于F,若DF=2$\sqrt{2}$,则EF=2. 如图,∠CAB=45°,AB=3,△ABC的面积为3,E为BC上任意一点,连AE,将△ABE,△ACE分别延AB,AC翻折至△ABM,△ACN,连MN,则MN的最小值$\frac{6}{5}$$\sqrt{10}$.
如图,∠CAB=45°,AB=3,△ABC的面积为3,E为BC上任意一点,连AE,将△ABE,△ACE分别延AB,AC翻折至△ABM,△ACN,连MN,则MN的最小值$\frac{6}{5}$$\sqrt{10}$. 如图,在⊙O中,半径OA⊥OB,弦AC∥BD,求证:AD⊥BC.
如图,在⊙O中,半径OA⊥OB,弦AC∥BD,求证:AD⊥BC. 如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+$\frac{12}{5}$与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M.
如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+$\frac{12}{5}$与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M.