题目内容
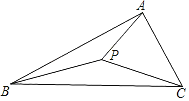
【题目】如图,在直角三角形△ABC内部有一动点P,∠BAC=90°,连接PA,PB,PC,若AC=6,AB=8,求PA+PB+PC的最小值_____.
【答案】![]()
【解析】
如图,将△ACP绕点C顺时针旋转60°得到△ECF,连接PF,BE,作EH⊥BA交BA的延长线于H.首先证明PA+PB+PC≥BE,求出BE的值即可解决问题.
如图,将△ACP绕点C顺时针旋转60°得到△ECF,连接PF,BE,作EH⊥BA交BA的延长线于H.
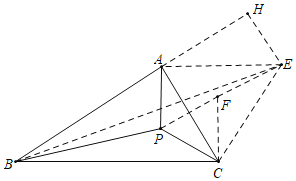
由旋转的旋转可知:PA=EF,△PCF,△ACE是等边三角形,
∴PF=PC,
∴PA+PB+PC=EF+FP+PB,
∵EF+FP+PB≥BE,
∴当B,P,F,E共线时,PA+PB+PC的值最小,
∵∠BAC=90°,∠CAE=60°,
∴∠HAE=180°﹣90°﹣60°=30°,
∵EH⊥AH,AE=AC=6,
∴EH=![]() AE=3.AH=
AE=3.AH=![]() EH=3
EH=3![]() ,
,
∴BE=![]() =
=![]() =
=![]() ,
,
∴PA+PB+PC的最小值为![]() .
.
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目