题目内容
如图,矩形OABC摆放在平面直角坐标系xOy中,点A在x轴上,点C在y轴上,OA=3,OC=2,P是BC边上一点且不与B重合,连结AP,过点P作∠CPD=∠APB,交x轴于点D,交y轴于点E,过点E作EF∥AP交x轴于点F.
(1)若△APD为等腰直角三角形,求点P的坐标;
(2)若以A,P,E,F为顶点的四边形是平行四边形,求直线PE的解析式.
(1)P(1,2);(2)PE的解析式为:y=2x﹣2
解析试题分析:(1)由等腰直角三角形的性质可知∠PAD=∠PDA=45°,再由矩形的性质求得∠1=∠2=45°,进而求得AB=BP=2即可求得.
(2)根据平行四边形的性质得出PD=DE,根据矩形的性质以及已知条件求得PD=PA,进而求得DM=AM,然后通过得出△PDM≌△EDO得出OD=DM=MA=1,EO=PM=2,即可求得.
试题解析:(1)如图1,∵△APD为等腰直角三角形,∴∠APD=90°,
∴∠PAD=∠PDA=45°,
又∵四边形ABCD是矩形,
∴OA∥BC,∠B=90°,AB=OC,
∴∠1=∠2=45°,
∴AB=BP,
又∵OA=3,OC=2,
∴BP=2,CP=1,
∴P(1,2),
(2)如图2∵四边形APFE是平行四边形,
∴PD=DE,
∵OA∥BC,
∴∠CPD=∠4,∠1=∠3,
∵∠CPD=∠1,
∴∠3=∠4,
∴PD=PA,
过P作PM⊥x轴于M,
∴DM=MA,
又∵∠PDM=∠EDO,∠PMD=∠EOD=90°,
在△PDM与△EDO中, ,
,
∴△PDM≌△EDO(AAS),
∴OD=DM=MA=1,EO=PM=2,
∴P(2,2),E(0,﹣2),
∴PE的解析式为:y=2x﹣2;

考点:一次函数综合题

某饮料厂开发了A、B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A、B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
| 原料名称 饮料名称 | 甲 | 乙 |
| A | 20克 | 40克 |
| B | 30克 | 20克 |
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?
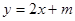 不经过第二象限,那么实数
不经过第二象限,那么实数 的取值范围是_________.
的取值范围是_________. 与反比例函数
与反比例函数 的图象交点的横坐标为x0.若k<x0<k+1,则整数k的值是 .
的图象交点的横坐标为x0.若k<x0<k+1,则整数k的值是 .



 (x>0)的图象交于点A(2,1),与x轴交于点B.
(x>0)的图象交于点A(2,1),与x轴交于点B.