题目内容
如图,已知直线AB与x轴、y轴分别交于A和B,OA=4,且OA、OB长是关于x的方程x2﹣mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM并延长交x轴于N.
(1)求⊙M的半径.
(2)求线段AC的长.
(3)若D为OA的中点,求证:CD是⊙M的切线.
(1)  ;(2)
;(2)  ;(3)证明见解析.
;(3)证明见解析.
解析试题分析:(1)由OA、OB长是关于x的方程x2﹣mx+12=0的两实根,得OA•OB=12,而OA=4,所以OB=3,又由于OB为⊙M的直径,即可得到⊙M的半径.
(2)连接OC,根据OB是⊙M直径,得到OC⊥BC,利用面积相等得到OC•AB=OA•OB可以求得OC的长,然后利用勾股定理求得AC的长即可.
(3)连MD,OC,由OB为⊙M的直径,得∠OCB=90°,则∠OCD=90°,由于D为OA的中点,所以CD= OA=OD,因此可证明△MCD≌△MOD,所以∠MCD=∠MOD=90°,即CD是⊙M的切线.
OA=OD,因此可证明△MCD≌△MOD,所以∠MCD=∠MOD=90°,即CD是⊙M的切线.
试题解析:(1)∵OA=4∴A(4,0)
又OA•OB长是x2﹣mx+12=0的两根
∴OA•OB=12∴OB=3 故B(0,3)
∵OB为直径
∴半径MB= ;
;
(2)连接OC
∵OB是⊙M直径
∴OC⊥BC
∴OC•AB=OA•OB
∵AB= ="5"
="5"
∴OC•5=3•4
∴OC=
∴AC=
(3)∵OM=MC∴∠MOC=∠MCO
又CD是Rt△OCA斜边上中线
∴DC=DO
∴∠DOC=∠DCO
∵∠DOC+∠MOC=90°
∴∠MCO+∠DCO=90°
∴DC⊥MC
∴CD是⊙M的切线
考点:一次函数综合题.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,超过部分按2.6元/m3计费。设每户家庭用水量为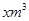 时,应交水费y元。
时,应交水费y元。
(1)分别求出 和
和 时y与x的关系式;
时y与x的关系式;
(2)小明家第二季度交纳水费的情况如下:
| 月份 | 四月份 | 五月份 | 六月份 |
| 交费金额 | 30元 | 34元 | 42.6元 |
 的图像相交于点P,则这个正比例函数的表达式是 .
的图像相交于点P,则这个正比例函数的表达式是 .

 与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.
与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.

 的图象交于A、B两点,与x轴交于D点,且C、D两点关于y轴对称.
的图象交于A、B两点,与x轴交于D点,且C、D两点关于y轴对称.
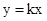 都会经过一个固定的点
都会经过一个固定的点 ,我们就称直线
,我们就称直线 取任何实数,抛物线
取任何实数,抛物线 恒过定点
恒过定点 ,直接写出定点A的坐标;
,直接写出定点A的坐标; ,且∠B,∠C的角平分线分别是y轴和直线
,且∠B,∠C的角平分线分别是y轴和直线 ,求边BC所在直线的表达式;
,求边BC所在直线的表达式;