��Ŀ����
ij���ϳ�������A��B�����������ϣ���Ҫԭ�Ͼ�Ϊ���ң�ÿƿ�����мס��ҵĺ������±���ʾ�����ü�ԭ�Ϻ���ԭ�ϸ�2800�˽������������ƻ�����A��B�������Ϲ�100ƿ��������A������xƿ�������������⣺
| ԭ������ �������� | �� | �� |
| A | 20�� | 40�� |
| B | 30�� | 20�� |
��1���м��ַ����������������д���������̣�
��2�����A������ÿƿ�ijɱ�Ϊ2.60Ԫ��B������ÿƿ�ijɱ�Ϊ2.80Ԫ�����������ϳɱ��ܶ�ΪyԪ����д��y��x֮��Ĺ�ϵʽ����˵��xȡ��ֵ��ʹ�ɱ��ܶ���ͣ�
��1��21�֣���2��y=-0.2x+280��x=40ʱ�ɱ��ܶ���ͣ�
���������������1��������A������xƿ�������ʽ�����鼴�ɣ�
��2����ͼ�ɵ�x��y�Ĺ�ϵʽ����֪��x��y�Ĺ�ϵ��
�����������1����������ã� ��
��
���������ʽ�飬��20��x��40��
���������������21����
���Է������������������21�֣�
��2���������⣬��y=2.6x+2.8��100-x����
��������y=-0.2x+280��
��k=-0.2��0��
��y��x�����������
�൱x=40ʱ�ɱ��ܶ���ͣ�
���㣺һԪһ�β���ʽ���Ӧ�ã�

ij��Ϊ�˹��������Լ��ˮ�����÷ֶμƷѵķ������¼���ÿ����ͥ��ˮ�ѣ�����ˮ��������20m3ʱ����2Ԫ/m3���㣻����ˮ������20m3ʱ���������ְ�2.6Ԫ/m3�Ʒѡ���ÿ����ͥ��ˮ��Ϊ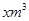 ʱ��Ӧ��ˮ��yԪ��
ʱ��Ӧ��ˮ��yԪ��
��1���ֱ���� ��
�� ʱy��x�Ĺ�ϵʽ��
ʱy��x�Ĺ�ϵʽ��
��2��С���ҵڶ����Ƚ���ˮ�ѵ�������£�
| �·� | ���·� | ���·� | ���·� |
| ���ѽ�� | 30Ԫ | 34Ԫ | 42.6Ԫ |
A���з���300�֣�B���з���200�֣���Ҫ����Щ����ȫ�������ף������磬��A�����ף��������˷��ϵķ��÷ֱ�Ϊÿ��20Ԫ��25Ԫ����B�����ף��������˷��ϵķ��÷ֱ�Ϊÿ��25Ԫ��15Ԫ���ּ�����Ҫ����260�֣�������Ҫ����240�֣����A����������ķ���Ϊx�֣�
��1�������������±��е�ÿһ�գ�
| ����� ���������֣� ������ | ���� | ���� | �ܼ� |
| A�� | x | ��_________�� | 300 |
| B�� | ��_________�� | ��_________�� | 200 |
| �ܼ� | 260 | 240 | 500 |
��3���������˻��ʣ���ʹ���˷����٣������˷��Ƕ��٣�
�±��У�y��x��һ�κ�����
| x |  2 2 | 1 | 2 | | 5 |
| y | 6 |  3 3 | |  12 12 |  15 15 |
��1����ú����ı���ʽ������ȫ����
��2����֪�ú���ͼ����һ��M��1��-3��Ҳ�ڷ���������
 ͼ���ϣ�������������ͼ�����һ����N�����꣮
ͼ���ϣ�������������ͼ�����һ����N�����꣮ 
 ��x�ύ�ڵ�A����y�ύ�ڵ�B������ABCD��ͼ������ƽ��ֱ������ϵ�У����е�D��x�Ḻ�����ϣ�ֱ��y=x+m������C����x���ڵ�E��
��x�ύ�ڵ�A����y�ύ�ڵ�B������ABCD��ͼ������ƽ��ֱ������ϵ�У����е�D��x�Ḻ�����ϣ�ֱ��y=x+m������C����x���ڵ�E��
 ��ͼ����A��B���㣬��x�ύ��D�㣬��C��D�������y��Գƣ�
��ͼ����A��B���㣬��x�ύ��D�㣬��C��D�������y��Գƣ�