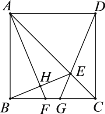题目内容
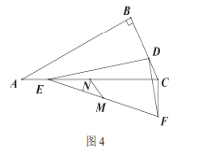
【题目】如图,在等腰△ABC中,AB=BC.CD∥AB,点D在点C的右侧,点A,E关于直线BD对称,CE交BD于点F,AE交DB延长线于点G.
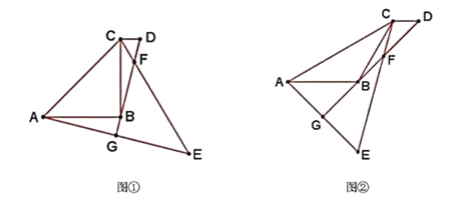
(1)(猜想)
如图①,当∠ABC=90°时,∠EFG=________;
(2)(探究)
在(1)的前提下,若AB=4,CD=1,求EF的长;
(3)(应用)
如图②,当∠ABC=120°时,若EF=2 ![]() ,AB=2,则CD=________.
,AB=2,则CD=________.
【答案】(1)45°;(2)EF= ![]() ;(3)
;(3)![]() -1
-1
【解析】
(1)连接BE,利用轴对称的性质得BE=BC=AB,然后利用等腰三角形的性质以及三角形内角、外角关系求解即可;
(2)易证△ABG∽△BCD,利用相似三角形的性质得AG:BC=AB:BD,据此求出AG.由轴对称性得GE=AG,由∠EFG=45°得EF=![]() AG,计算即可得到答案;
AG,计算即可得到答案;
(3)连接BE,过点C作CH⊥GD于H,同(1)可得∠BEF=∠BCE=∠CBF=15°,进而得BF=CF=![]() ,则CH=
,则CH=![]() ,进而得CD=
,进而得CD=![]() CH,故可求.
CH,故可求.
(1)连接BE,如图所示:
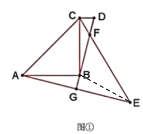
因为点A,E关于直线BD对称,且AB=BC,所以利用轴对称的性质得BE=BC=AB,且![]() .由等腰三角形的性质可得
.由等腰三角形的性质可得![]() ,
,![]() ,又因为三角形ACE的内角等于
,又因为三角形ACE的内角等于![]() ,且∠ABC=90°,AB=BC,所以三角形ACE的内角等于
,且∠ABC=90°,AB=BC,所以三角形ACE的内角等于![]() ,所以
,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,又因为
,又因为![]() ,所以∠EFG=45°.
,所以∠EFG=45°.
(2)解:∵CD∥AB,∴∠D=∠ABG.
又∠AGB=∠BCD=∠ABC=90°,
∴△ABG∽△BCD,
又∵AB=4,CD=1,AB=BC,
∴BD=![]() ,AB=BC=4,
,AB=BC=4,
∴AG:BC=AB:BD,可以得到AG= ![]() .由对称性,得GE=AG=
.由对称性,得GE=AG= ![]() .又由∠EFG=45°得EF=
.又由∠EFG=45°得EF=![]() AG,∴EF
AG,∴EF![]() =
= ![]() .
.
(3)连接BE,过点C作CH⊥GD于H,如下图所示:
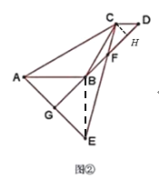
同(1)可得∠BEF=∠BCE=∠CBF=15°,进而得BF=CF=![]() ,则CH=
,则CH=![]() ,进而得CD=
,进而得CD=![]() CH,故可求CD=
CH,故可求CD=![]() =
=![]() -1.
-1.

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案