题目内容
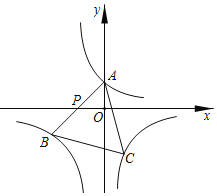
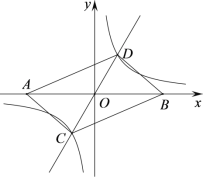
【题目】如图,在平面直角坐标系中,点A的坐标为(m,0),m<0,点B与点A 关于原点对称,直线![]() 与双曲线
与双曲线![]() 交于C,D两点.
交于C,D两点.
(1)直接判断后填空:四边形ACBD的形状一定是 ;
(2)若点D(1,t),求双曲线的解析式;
(3)在(2)的前提下,四边形ACBD为矩形时,求m的值.
【答案】(1)平行四边形;(2)![]() ;(3)m=-2
;(3)m=-2
【解析】
(1)根据正、反比例函数的对称性即可得出点D、C关于原点O成中心对称,再结合点A与点B关于坐标原点O成中心对称,即可得出对角线AB、CD互相平分,由此即可证出四边形ACBD的是平行四边形;
(2)由点D的坐标结合反比例函数图象上点的坐标特征即可求出t值,进而得出点A的坐标,代入双曲线即可求出解析式.
(3)根据勾股定理得出OD长度,再根据矩形的性质可得出OB=OA=OC=OD=2,得到点A的坐标即可求出m值;
(1)平行四边形;
(2)将D(1,t)代入![]() 中
中
求得:t=![]() ,D(1,
,D(1,![]() )
)
k=xy=1×![]() =
=![]()
∴反比例函数解析式是:![]()
(3)由勾股定理求得OD=2,
∵四边形ACBD为矩形
∴OA=OB=OC=OD=2
∵m<0
∴m=-2.

练习册系列答案
相关题目