题目内容
【题目】在学习《圆》这一单元时,我们学习了圆周角定理的推论:圆内接四边形的对角互补;事实上,它的逆命题:对角互补的四边形的四个顶点共圆,也是一个真命题.在图形旋转的综合题中经常会出现对角互补的四边形,那么,我们就可以借助“对角互补的四边形的四个顶点共圆”,然后借助圆的相关知识来解决问题,例如:
已知:![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 内一点,连接
内一点,连接![]() ,将线段
,将线段![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() .当点
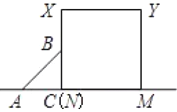
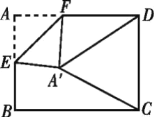
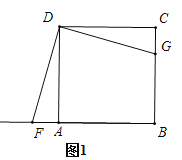
.当点![]() 在如图所示的位置时:
在如图所示的位置时:
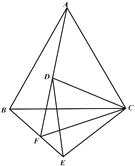
(1)观察填空:
①与![]() 全等的三角形是________;
全等的三角形是________;
②![]() 的度数为
的度数为
(2)利用题干中的结论,证明:![]() ,
,![]() ,
,![]() ,
,![]() 四点共圆;
四点共圆;
(3)直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系.____________________.
之间的数量关系.____________________.
【答案】(1)①![]() :②
:②![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)①根据旋转的性质和等边三角形的性质可证△ACD≌△BCE;
②根据已推导出的全等三角形和三角形内角和进行角度转化,可得∠AFB的大小;
(2)根据△ACD≌△BCE得![]() ,推导得出四边形CDFE中
,推导得出四边形CDFE中![]() ,从而证共圆;
,从而证共圆;
(3)先推导出△BDF是等边三角形,可证△ABD≌△CBP,得出AD=FC,从而得出数量关系.
(1)①∵△ABC是等边三角形
∴AB=AC=BC,∠BAC=∠ACB=∠ABC=60°
∵将线段![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]()
∴CE=CD,∠DCE=60°
∴△DCE是等边三角形
∴∠DCE=60°
∵∠ACD+∠DCB=60°,∠BCE+∠DCB=60°
∴∠ACD=∠BCE
∴△ACD≌△BCE(SAS)
②∵△ACD≌△BCE
∴∠EBC=∠DAC
∵∠DAC+∠BAD=∠BAC=60°
∴∠FBC+∠BAD=60°
∴∠AFB=180°-∠ABC-∠FBC-∠BAF=180°-60°-60°=60°
(2)∵![]() .
.
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() ,
,![]() ,
,![]() ,
,![]() 四点共圆;
四点共圆;
(证明不唯一)
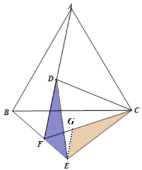
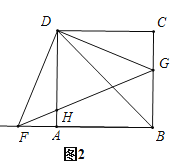
(3)结论:![]() ,如下图,连接BD
,如下图,连接BD
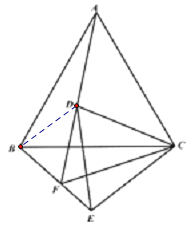
∵△ACD≌△BCE
∴∠CBE=∠CAD,AD=BE
∵∠CAD+∠BAD=60°,∠BAD+∠FBC=60°
∴∠BAD+∠ABD=∠BDF=60°
∵∠AFB=60°
∴△BDF是等边三角形
∴DF=BF,∴FD+FE=BE
∴△ABD≌△CBF(SAS)
∴AD=FC
∴FD+FE=FC

【题目】有这样一个问题:探究函数![]() 的图象与性质,小李根据学习函数的经验,对函数
的图象与性质,小李根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小李探究的过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是______;
的取值范围是______;
(2)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
| … |
|
|
| 0 | 2 | 3 | 4 | 5 | … |
| … | 0 |
|
|
| 5 | 3 |
| 2 | … |
则![]() 的值为_______;
的值为_______;
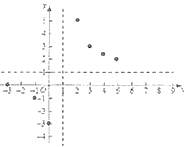
(3)如图所示,在平面直角坐标系![]() 中,根据描出的点,请补全此函数的图象;
中,根据描出的点,请补全此函数的图象;
(4)观察图象,写出该函数的一条性质_______;
(5)若函数![]() 的图象在函数
的图象在函数![]() 的图象上方,直接写出
的图象上方,直接写出![]() 的取值范围_______.
的取值范围_______.