题目内容
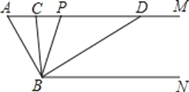
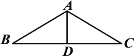
【题目】在矩形ABCD中,AB=4,BC=10,E是直线AD上任意一点(不与点A重合),点A关于直线BE的对称点为A′,AA′所在直线与直线BC交于点F.
(1)如图①,当点E在线段AD上时,①若△ABE ∽△DEC,求AE的长;
②设AE=x,BF=y,求y与x的函数表达式.
(2)线段DA′的取值范围是 .


【答案】(1)①2或8;②y=![]() ;(2)
;(2)![]() ≤DA′≤
≤DA′≤![]() .
.
【解析】分析:(1)①设AE=x,再根据对应边成比例可得到关于x的一元二次方程,求解即可;②由![]() ,推出
,推出![]() ,由对应线段成比例得到关于x, y的方程,变形即可;(2)对称轴和对称点连线的交点在以线段AB为直径的圆上,D
,由对应线段成比例得到关于x, y的方程,变形即可;(2)对称轴和对称点连线的交点在以线段AB为直径的圆上,D![]() 最短时 ,
最短时 , ![]() 在对角线BD.
在对角线BD.
本题解析:
(![]() )①设
)①设![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() 或
或![]() .
.

②∵![]() 是
是![]() 所在直线与直线
所在直线与直线![]() 的交点,且
的交点,且![]() 与
与![]() 关于直线
关于直线![]() 对称,
对称,
∴![]() ,
,
设![]() 与
与![]() 交于点
交于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() .
.
(![]() )
)![]()

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
【题目】某公司有A、B两种型号的客车,它们的载客量、每天的租金如表所示:
A型号客车 | B型号客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 600 | 450 |
已知某中学计划租用A、B两种型号的客车共10辆,同时送七年级师生到沙家参加社会实践活动,已知该中学租车的总费用不超过5600元.
(1)求最多能租用多少辆A型号客车?
(2)若七年级的师生共有380人,请写出所有可能的租车方案.