Question

【题目】在ABCD中，E是AD上一点，AE=AB，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG．

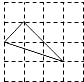
（1）如图1，当EF与AB相交时，若∠EAB=60°，求证：EG=AG+BG；

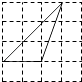
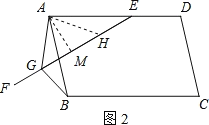
（2）如图2，当EF与AB相交时，若∠EAB=α（0°＜α＜90°），请你直接写出线段EG、AG、BG之间的数量关系（用含α的式子表示）；

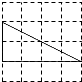
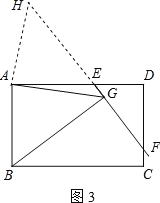
（3）如图3，当EF与CD相交时，且∠EAB=90°，请你写出线段EG、AG、BG之间的数量关系，并证明你的结论．

Answer 1

【答案】（1）证明见解析（2）（3）

【解析】试题分析：（1）首先作交于点H，易证得≌，又由，可证得是等边三角形，继而证得结论；
（2）首先作交于点H，作于点，易证得

≌，又由 易得，继而证得结论；
（3）首先作交于点H，易证得≌，继而可得是等腰直角三角形，则可求得答案．

试题解析：(1)证明：如图，作∠GAH=∠EAB交GE于点H.

∴∠GAB=∠HAE.

∵∠EAB=∠EGB，∠APE=∠BPG，

∴∠ABG=∠AEH.

在△ABG和△AEH中，

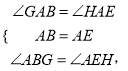
∴≌ (ASA).

∴BG=EH，AG=AH.

∴△AGH是等边三角形，

∴AG=HG.

∴EG=AG+BG.

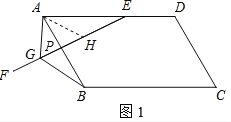
(2)如图，作∠GAH=∠EAB交GE于点H.作AM⊥EG于点M，

∴∠GAB=∠HAE.

∵∠EAB=∠EGB，∠APE=∠BPG，

∴∠ABG=∠AEH.

在△ABG和△AEH中，

∴≌ (ASA).

∴BG=EH，AG=AH.

∵∠GAH=∠EAB=α，

∴EG=GH+BG.

(3)

如图，作∠GAH=∠EAB交GE于点H.

∴∠GAB=∠HAE.

∴∠ABG=∠AEH.

∵又AB=AE，

∴△ABG≌△AEH.

∴BG=EH，AG=AH.

∴△AGH是等腰直角三角形.