题目内容
【题目】一条笔直跑道上的A,B两处相距500米,甲从A处,乙从B处,两人同时相向匀速而跑,直到乙到达A处时停止,且甲的速度比乙大.甲、乙到A处的距离![]() (米)与跑动时间
(米)与跑动时间![]() (秒)的函数关系如图14所示.
(秒)的函数关系如图14所示.
(1)若点M的坐标(100,0),求乙从B处跑到A处的过程中![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)若两人之间的距离不超过200米的时间持续了40秒.
①当![]() 时,两人相距200米,请在图14中画出P(
时,两人相距200米,请在图14中画出P(![]() ,0).保留画图痕迹,并写出画图步骤;
,0).保留画图痕迹,并写出画图步骤;
②请判断起跑后![]() 分钟,两人之间的距离能否超过420米,并说明理由.
分钟,两人之间的距离能否超过420米,并说明理由.

【答案】(1)![]() ;(2)①见解析;②起跑后
;(2)①见解析;②起跑后![]() 分钟,两人之间的距离不能超过
分钟,两人之间的距离不能超过![]() 米,理由见解析.
米,理由见解析.
【解析】
(1)设乙从B处跑到A处的过程中y与x的函数关系式为y=kx+b,把(0,500)和(100,0)代入求出k,b的值即可,
(2)①设![]() ,两直线相交于点
,两直线相交于点![]() .过点
.过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,
,
在射线![]() 上截取
上截取![]() ,使
,使![]() 过点
过点![]() 作
作![]() 轴的垂线,则垂足
轴的垂线,则垂足![]() 即为所求点.
即为所求点.
②由两人有相距200到相遇用时50秒,由a>b,![]() ,起跑后
,起跑后![]() 分钟(即
分钟(即![]() 秒),两人处于相遇过后,但乙未到达
秒),两人处于相遇过后,但乙未到达![]() 处,则计算乙在90秒内离开B距离比较即可.
处,则计算乙在90秒内离开B距离比较即可.
(1)设![]()
把![]() 分别代入,可求得
分别代入,可求得![]()
∴解析式为![]()
(2)如图:
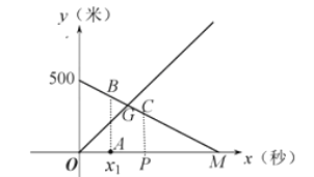
设![]() ,两直线相交于点
,两直线相交于点![]() .
.
步骤为: .
①过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]()
②在射线![]() 上截取
上截取![]() ,使
,使![]()
③过点![]() 作
作![]() 轴的垂线,则垂足
轴的垂线,则垂足![]() 即为所求点.
即为所求点.
(3)起跑后![]() 分钟,两人之间的距离不能超过
分钟,两人之间的距离不能超过![]() 米.
米.
理由如下:
由题可设![]()
∵两人之间的距离不超过![]() 米的时间持续了
米的时间持续了![]() 秒,
秒,
∴可设当![]() 或
或![]() 时,两人相距为
时,两人相距为![]() 米.
米.
∴相遇前,当![]() 时,
时,![]() ,即
,即![]()
也即![]() ①.
①.
相遇后,当![]() 时,
时, ![]()
即![]()
也即![]() ②.
②.
把①代入②,可得![]()
解得![]()
当两人相遇时,![]() ,即
,即![]()
即![]() ,解得x=50.
,解得x=50.
∵甲的速度比乙大,所以![]() ,可得
,可得![]()
∴起跑后![]() 分钟(即
分钟(即![]() 秒),两人处于相遇过后,但乙未到达
秒),两人处于相遇过后,但乙未到达![]() 处.
处.
∴两人相距为![]()
∵![]() ,
,
∴两人之间的距离不能超过![]() 米.
米.

练习册系列答案
相关题目