题目内容
【题目】如图,我把对角线互相垂直的四边形叫做“垂美四边形”.
(1)性质探究:如图1.已知四边形ABCD中,AC⊥BD,垂足为O,求证:AB2+CD2=AD2+BC2.
(2)解决问题:已知AB=5,BC=4,分别以△ABC的边BC和AB向外作等腰Rt△BCQ和等腰Rt△ABP.
①如图2,当∠ACB=90°,连接PQ,求PQ;
②如图3,当∠ACB≠90°,点M、N分别是AC、AP中点连接MN.若MN=![]() ,则S△ABC= .
,则S△ABC= .

【答案】(1)详见解析;(2)①![]() ,②
,②![]()
【解析】
(1)利用勾股定理即可得出结论;
(2)①根据SAS可证明△PBC≌△ABQ,得∠BPC=∠BAQ,得∠PDA=90°,可求出PQ的长;
②连接PC、AQ交于点D,同①可证△PBC≌△ABQ,则AQ=PC且AQ⊥PC,由MN=2![]() ,可知AQ=PC=4
,可知AQ=PC=4![]() .延长QB作AE⊥QE,求出BE的长,则答案可求出.
.延长QB作AE⊥QE,求出BE的长,则答案可求出.
解:(1)证明:如图中,

∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AB2+CD2=AD2+BC2;
(2)①如图,连接PC、AQ交于点D,
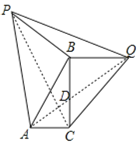
∵△ABP和△CBQ都是等腰直角三角形,
∴PB=AB,CB=BQ,∠ABP=∠CBQ=90°,
∴∠PBC=∠ABQ,
∴△PBC≌△ABQ(SAS),
∴∠BPC=∠BAQ,
又∵∠BPC+∠CPA+∠BAP=90°,
即∠BAQ+∠CPA+∠BAP=90°,
∴∠PDA=90°,
∴PC⊥AQ,
利用(1)中的结论:AP2+CQ2=AC2+PQ2
即(5![]() )2+(4
)2+(4![]() )2=32+PQ2;
)2=32+PQ2;
∴PQ=![]() .
.
②如图,连接PC、AQ交于点D,
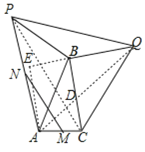
同①可证△PBC≌△ABQ(SAS),AQ=PC且AQ⊥PC,
∵M、N分别是AC、AP中点,
∴MN=![]() ,
,
∵MN=2![]() ,
,
∴AQ=PC=4![]() .
.
延长QB作AE⊥QE,
则有AE2+BE2=25,AE2+QE2=48,
∵EQ=4+BE,
∴(4+BE)2﹣BE2=23,
解得BE=![]() ,
,
∴S△ABC=![]() BC×BE=
BC×BE=![]() =
=![]() .
.
故答案为:![]() .
.







