题目内容
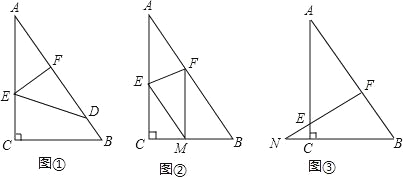
【题目】已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON,垂足为点F.
(1)如图(1),作AE⊥ON,垂足为点E. 当m=2时,求线段EF的长度;
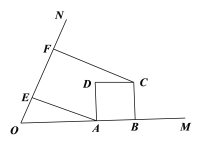
图(1)
(2)如图(2),联结OC,当m=2,且CD平分∠FCO时,求∠COF的正弦值;
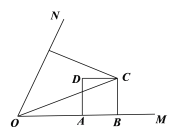
图(2)
(3)如图(3),当△AFD与△CDF相似时,求m的值.
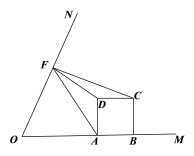
图(3)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)1或2或
;(3)1或2或![]() .
.
【解析】
(1)如图1,延长FC交OM于点G,证∠BCG=∠MON,在Rt△AOE中,设OE=a,可求得OA,OG,OF的长,则![]() ;
;
(2)如图2,延长FC交OM于点G,由(1)得![]() ,推出
,推出![]() ,在Rt△COB中,由勾股定理求出a的值,得出OF的长,可求出cos∠COF的值,进一步推出sin∠COF的值;
,在Rt△COB中,由勾股定理求出a的值,得出OF的长,可求出cos∠COF的值,进一步推出sin∠COF的值;
(3)需分情况讨论:当D在∠MON内部时,△FDA∽△FDC时,此时CD=AD=2,m=2;当△FDA∽△CDF时,延长CD交ON于点Q,过F作FP⊥CQ于P,可利用三角函数求出m的值;当D在∠MON外部时,可利用相似的性质等求出m的值.
解:解:(1)如图1,
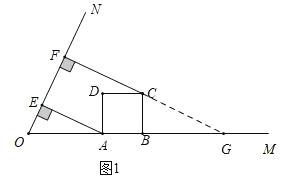
延长![]() 交
交![]() 于点
于点![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
则![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,
设![]() ,由
,由![]() ,
,
可得![]() ,则
,则![]() ,
,![]() ,
,
![]() ;
;
(2)如图2,
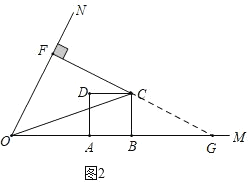
延长![]() 交
交![]() 于点
于点![]() ,由(1)得
,由(1)得![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,由
中,由![]() ,
,
得![]() ,
,
解得![]() (舍去),
(舍去),![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)当![]() 在
在![]() 内部时,
内部时,
①如图![]() ,
,
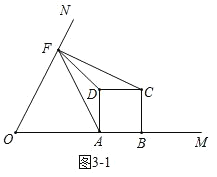
![]() 时,此时
时,此时![]() ,
,
![]() ;
;
②当![]() 时,
时,
如图![]() ,
,
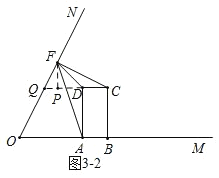
延长![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ;
;
当![]() 在
在![]() 外部时,
外部时,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
如图![]() ,
,
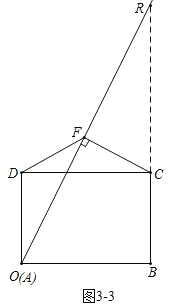
![]() 时,此时
时,此时![]() ,
,
![]() ,
,
![]() ,
,
![]() 、
、![]() 重合,
重合,
延长![]() 交
交![]() 于
于![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ;
;
如图![]() ,
,
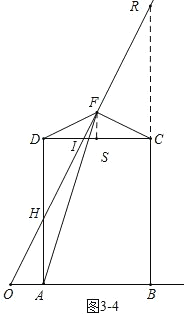
![]() 时,设
时,设![]() ,
,
延长![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
解得,![]() ,
,![]() (舍去),
(舍去),
![]() ,矛盾,
,矛盾,
综上所述:![]() 或
或![]() ,或
,或![]() .
.

练习册系列答案
相关题目