��Ŀ����
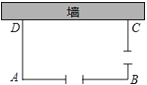
����Ŀ����ͼ������һ�泤Ϊ34��ǽ������դ��Χ��һ���������г�����ABCD����AB��BC�߸���һ��2����С�ţ�������դ�����������ABCD�ı�AD��Ϊx�ף�AB��Ϊy�ף����ε����ΪSƽ���ף���x��y��
��1����������դ���ij�Ϊ40�ף���y��x�ĺ�����ϵʽ����ֱ��д���Ա���x��ȡֵ��Χ��
��2���ڣ�1���������£���S��x�ĺ�����ϵʽ�����������Χ����ʹ���γ��ص����Ϊ192ƽ���ף�
���𰸡���1��![]() ����2��
����2��![]() ��AD=6�ף�AB=32�ף�
��AD=6�ף�AB=32�ף�
��������
���⣨1����34��ǽ����2����С�ţ��õ�ƽ����ǽ�ıߣ��Լ���ֱ��ǽ��������֮�ͣ���AD=x��AB=y��������դ���ij�Ϊ40�ף����������֮�ͱ�ʾ��y��x�Ĺ�ϵʽ��
��2���ɣ�1����ʾ����y��x�Ĺ�ϵʽ���г�S��x�ĺ�����ϵʽ�����ݾ��γ��ص����Ϊ192ƽ���ף����AD��AB�ij����ɣ�
����������⣺��1����y+2x-2��2=40,
��y=-2x+44,
��5��x��![]() ��
��
��2����y=-2x+44,
��S=xy=x��-2x+44��=-2x2+44x��
�����γ��ص����Ϊ192ƽ���ף�
��-2x2+44x=192��
��x=6��x=16���������⣩��
��AB=y=-2x+44=-2��6+44=32��
��AD=6�ף�AB=32�ײ���ʹ���γ��ص����Ϊ192ƽ���ף�

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�����Ŀ��������ѧ�����ʽ��������涨�����ʲ��Գɼ��ﵽ90.0�ּ����ϵ�Ϊ���㣻�ﵽ80.0����89.9�ֵ�Ϊ���ã��ﵽ60.0����79.9�ֵ�Ϊ����59.9�ּ�����Ϊ������ijУΪ���˽���꼶ѧ�����ʽ���״�����Ӹ�У���꼶ѧ���������ȡ��10%��ѧ���������ʲ��ԣ����Խ���������ͳ�Ʊ�������ͳ��ͼ��ʾ��
���ȼ�ѧ��ƽ����ͳ�Ʊ�
�ȼ� | ���� | ���� | ���� | ������ |
ƽ���� | 92.1 | 85.0 | 69.2 | 41.3 |
���ȼ�ѧ�������ֲ�����ͳ��ͼ

��1������ͳ��ͼ��������������ռ�İٷֱ��� ��;
��2����������ȡ��ѧ���IJ��Գɼ���ƽ���֣�
��3��������ȡ��ѧ�������в�����ȼ�ѧ�����ܷ�ǡ�õ���ijһ�����õȼ�ѧ���ķ���������Ƹþ��꼶ѧ����Լ�ж����˴ﵽ����ȼ���
����Ŀ�����κ���![]() ��
��![]() �dz�����
�dz�����![]() �����Ա���
�����Ա���![]() �뺯��ֵ
�뺯��ֵ![]() �IJ��ֶ�Ӧֵ���±���
�IJ��ֶ�Ӧֵ���±���
| �� |
|
| 0 | 1 | 2 | �� |
| �� |
|
|
|
|
| �� |
�ҵ�![]() ʱ�������Ӧ�ĺ���ֵ
ʱ�������Ӧ�ĺ���ֵ![]() �������н��ۣ���
�������н��ۣ���![]() ����
����![]() ��3�ǹ���
��3�ǹ���![]() �ķ���
�ķ���![]() ������������
������������![]()
![]() �����У���ȷ���۵ĸ����ǣ� ��
�����У���ȷ���۵ĸ����ǣ� ��
A. 0B. 1C. 2D. 3