��Ŀ����
����Ŀ����֪����y=ax2+bx+c(b<0)����ֻ��һ��������.
(1)������������Ϊ(2��0)����a��c����Ĺ�ϵʽ��
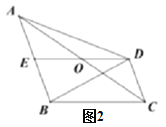
(2)��AΪ�������ϵ�һ���㣬ֱ��l��y=kx+1��k�������߽��ڵ�B��C���㣬ֱ��BD��ֱ��ֱ��y=��1,����Ϊ��D.��k��0ʱ��ֱ��l�������ߵ�һ��������y���ϣ�����ABCΪ����ֱ��������.
�����A������������ߵĽ���ʽ��
��֤��������ÿ��������ʵ��k������A��D��C���㹲��.
���𰸡�(1) y=a(x��2)2, c=4a;(2) �ٶ���A(1,0)��y= x2��2x+1,�ڼ�����.
��������
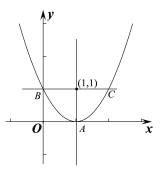
��1��������������x��Ĺ��������꼴Ϊ�����������꣬������⣻
��2����y��kx��1k��k��x1����1�����㣨1��1�����ҵ�k��0ʱ��ֱ��l��Ϊy��1ƽ��x�ᣬ����Ľ���Ϊ��0��1����������⣻�ڼ���ֱ��AD����ʽ�е�kֵ��ֱ��AC����ʽ�е�kֵ������kֵ��ȼ�����⣮
�⣺��1����������x��Ĺ��������꼴Ϊ�����������꣬�ʣ�y��a��x2��2����c��4a��
(2) y=kx+1��k= k(x��1)+1������(1,1),
�ҵ�k��0ʱ��ֱ��l��Ϊy=1ƽ��x��,��y��Ľ���Ϊ(0,1)
����ABCΪ����ֱ�������Σ����AΪ�����ߵĶ���
��c=1������A(1,0)
�����ߵĽ���ʽ: y= x2��2x+1.
��![]()
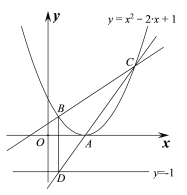
x2��(2+k)x+k��0,
x��![]() (2+k��
(2+k��![]() )
)
xD��xB��![]() (2+k��
(2+k��![]() ), yD=��1��
), yD=��1��
��D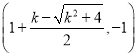
yC��![]() (2+k2+k
(2+k2+k![]() ,
,
C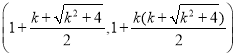 ��A(1,0)
��A(1,0)
��ֱ��AD����ʽ�е�kֵΪ��k AD=![]() =
=![]() ��
��
ֱ��AC����ʽ�е�kֵΪ��k AC=![]()
��k AD= k AC, ��A��C��D���㹲��.