题目内容
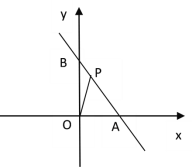
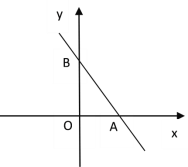
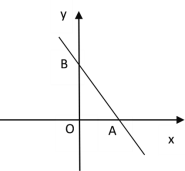
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
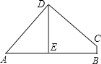
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

【答案】(1)抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+2
x+2
(2)存在,P1(![]() ,4),P2(
,4),P2(![]() ,
,![]() ),P3(
),P3(![]() ,﹣
,﹣![]() )
)
(3)当点E运动到(2,1)时,四边形CDBF的面积最大,S四边形CDBF的面积最大=![]() .
.
【解析】
试题(1)将点A、C的坐标分别代入可得二元一次方程组,解方程组即可得出m、n的值;
(2)根据二次函数的解析式可得对称轴方程,由勾股定理求出CD的值,以点C为圆心,CD为半径作弧交对称轴于P1;以点D为圆心CD为半径作圆交对称轴于点P2,P3;作CH垂直于对称轴与点H,由等腰三角形的性质及勾股定理就可以求出结论;
(3)由二次函数的解析式可求出B点的坐标,从而可求出BC的解析式,从而可设设E点的坐标,进而可表示出F的坐标,由四边形CDBF的面积=S△BCD+S△CEF+S△BEF可求出S与a的关系式,由二次函数的性质就可以求出结论.
试题解析:(1)∵抛物线y=﹣![]() x2+mx+n经过A(﹣1,0),C(0,2).
x2+mx+n经过A(﹣1,0),C(0,2).
解得: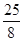 ,
,
∴抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)∵y=﹣![]() x2+
x2+![]() x+2,
x+2,
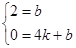
∴y=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴抛物线的对称轴是x=![]() .
.
∴OD=![]() .
.
∵C(0,2),
∴OC=2.
在Rt△OCD中,由勾股定理,得
CD=![]() .
.
∵△CDP是以CD为腰的等腰三角形,
∴CP1=CP2=CP3=CD.
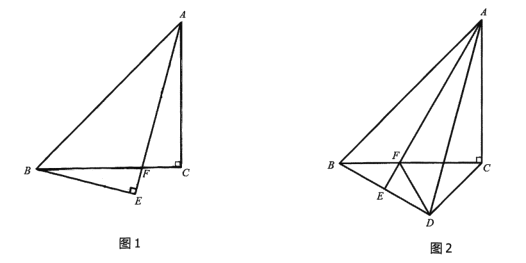
作CH⊥x轴于H,
∴HP1=HD=2,
∴DP1=4.
∴P1(![]() ,4),P2(
,4),P2(![]() ,
,![]() ),P3(
),P3(![]() ,﹣
,﹣![]() );
);
(3)当y=0时,0=﹣![]() x2+
x2+![]() x+2
x+2
∴x1=﹣1,x2=4,
∴B(4,0).
设直线BC的解析式为y=kx+b,由图象,得
![]() ,
,
解得: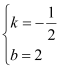 ,
,
∴直线BC的解析式为:y=﹣![]() x+2.
x+2.
如图2,过点C作CM⊥EF于M,设E(a,﹣![]() a+2),F(a,﹣
a+2),F(a,﹣![]() a2+
a2+![]() a+2),
a+2),
∴EF=﹣![]() a2+
a2+![]() a+2﹣(﹣
a+2﹣(﹣![]() a+2)=﹣
a+2)=﹣![]() a2+2a(0≤x≤4).
a2+2a(0≤x≤4).
∵S四边形CDBF=S△BCD+S△CEF+S△BEF=![]() BDOC+
BDOC+![]() EFCM+
EFCM+![]() EFBN,
EFBN,
=![]() +
+![]() a(﹣
a(﹣![]() a2+2a)+
a2+2a)+![]() (4﹣a)(﹣
(4﹣a)(﹣![]() a2+2a),
a2+2a),
=﹣a2+4a+![]() (0≤x≤4).
(0≤x≤4).
=﹣(a﹣2)2+![]()
∴a=2时,S四边形CDBF的面积最大=![]() ,
,
∴E(2,1).