Question

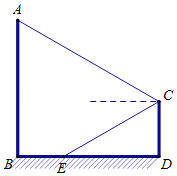
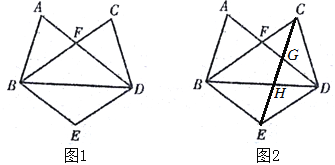
【题目】如图，AD与BC相交于点F，FA=FC，∠A=∠C，点E在BD的垂直平分线上．

（1）如图1，求证：∠FBE=∠FDE；

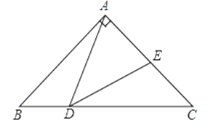
（2）如图2，连接CE分别交BD、AD于点H、G，当∠FBD=∠DBE=∠ABF，CD=DE时，直接写出所有与△ABF全等的三角形．

Answer 1

【答案】（1）证明见解析；（2）△DFC、△BEH、△CHD、△EDG.

【解析】试题分析：

（1）由题意易证△ABF≌△CDF，由此可得：BF=DF，从而可得∠FBD=∠FDB；由点E在BD的垂直平分线上可得BE=DE，由此可得∠EBD=∠EDB，这样即可得到∠FBE=∠FDE；

（2）由（1）中结论结合∠FBD=∠DBE=∠ABF，CD=DE易证△BFD≌△BED，由此可证得AB=CD=DE=BE=BF=DF，设∠ABF=2x，则可得∠A=∠BFA=90°-x，∠FBD=∠FDB=2x由此可得∠AFB=4x，这样在△ABF中由三角形内角和定理可得：2x+90-x+4x=180，由此可得x=18°，这样即可证得△ABF，△DCF，△BEH，△DEG和△CDH都是顶角为36°的等腰三角形，结合AB=CD=DE=BE即可得到这5个三角形全等，即与△ABF全等的三角形有4个.

试题解析：

（1）∵在△ABF和△CDF中，∠A=∠C，AF=CF，∠AFB=∠CFD，

∴△ABF≌△CDF，

∴BF=DF，

∴∠FBD=∠FDB，

∵由点E在BD的垂直平分线上，

∴BE=DE，

∴∠EBD=∠EDB，

∴∠FBD+∠EBD=∠FDB+∠EDB，即∠FBE=∠FDE；

（2）由（1）可知∠ABF=∠CDF，∠FBE=∠FDE，AB=CD，

∵∠FBD=∠DBE=∠ABF，CD=DE

∴∠ABF=∠FBD=∠EBD=∠CDF=∠FDB=∠BDE，AB=CD=DE=BE，

∴△BFD≌△BED，

∴BF=BE，

∴AB=BF=BE=DE=CD=DF，

∴若设∠ABF=2x，则可得∠A=∠AFB=90°-x，∠FBD=∠FDB=2x，

∵∠AFB=∠FBD+∠FDB=4x，

∴4x=90-x，解得x=18°，

由此可得∠ABF=2x=36°，∠A=∠AFB=72°，即△ABF是顶角为36°的等腰三角形，

结合∠ABF=∠FBD=∠EBD=∠CDF=∠FDB=∠BDE，AB=BF=BE=DE=CD=DF计算可得△DCF，△BEH，△DEG和△CDH都是顶角为36°的等腰三角形，且它们和△ABF有一腰是相等的，

∴△ABF，△DCF，△BEH，△DEG和△CDH是相互全等的，即与△ABF全等的三角形有4个，分别是△DCF，△BEH，△DEG和△CDH.