题目内容
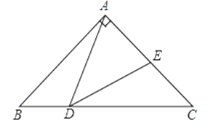
【题目】如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.
(1)求证:△ABD∽△DCE;
(2)当△ADE是等腰三角形时,求AE的长.
【答案】(1)见解析;(2)1
【解析】
(1)首先根据等腰直角三角形的两个底角都是45![]() ,得到一对对应角相等;再根据三角形的外角的性质得到∠ADE+∠EDC=∠B+∠BAD,从而证明∠EDC=∠BAD,根据两个角对应相等,得到两个三角形相似;
,得到一对对应角相等;再根据三角形的外角的性质得到∠ADE+∠EDC=∠B+∠BAD,从而证明∠EDC=∠BAD,根据两个角对应相等,得到两个三角形相似;
(2)根据等腰三角形的定义,此题要分AD=AE、AD=DE、AE=DE三种情况进行分析讨论.
(1)证明:Rt△ABC中,∠BAC=90°,AB=AC=2,
∴∠B=∠C=45°.
∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,
∴∠ADE+∠EDC=∠B+∠BAD.
又∵∠ADE=45°,
∴45°+∠EDC=45°+∠BAD.
∴∠EDC=∠BAD.
∴△ABD∽△DCE.
(2)解:讨论:①若AD=AE时,∠DAE=90°,此时D点与点B重合,不合题意.
②若AD=DE时,△ABD与△DCE的相似比为1,此时△ABD≌△DCE,
于是AB=AC=2,BC=2![]() ,AE=AC﹣EC=2﹣BD=2﹣(2
,AE=AC﹣EC=2﹣BD=2﹣(2![]() ﹣2)=4﹣2
﹣2)=4﹣2![]()
③若AE=DE,此时∠DAE=∠ADE=45°,
如下图所示易知AD⊥BC,DE⊥AC,且AD=DC.由等腰三角形的三线合一可知:AE=CE=![]() AC=1.
AC=1.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目