题目内容
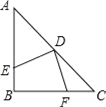
【题目】如图所示，已知 AD//BC, 点 E 为 CD 上一点，AE、BE 分别平分∠DAB、∠CBA,BE交 AD 的延长线于点 F.求证：（1）△ABE≌△AEF;(2) AD+BC=AB
【答案】见解析
【解析】
（1）根据角平分线的定义可得∠1=∠2，∠3=∠4，再根据两直线平行，内错角相等可得∠2=∠F，然后求出∠1=∠F，再利用“角角边”证明△ABE和△AFE全等即可；
（2）根据全等三角形对应边相等可得BE=FE，然后利用“角边角”证明△BCE和△FDE全等，根据全等三角形对应边相等可得BC=DF，然后根据AD+BC整理即可得证．
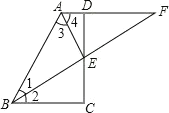(1)证明：如图，∵AE、BE分别平分∠DAB、∠CBA，
∴∠1=∠2，∠3=∠4，
∵AD∥BC，
∴∠2=∠F，∠1=∠F，
在△ABE和△AFE中，
∴△ABE≌△AFE(AAS)；
(2)证明：∵△ABE≌△AFE，
∴BE=EF，
在△BCE和△FDE中，
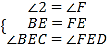
∴△BCE≌△FDE(ASA)，
∴BC=DF，
∴AD+BC=AD+DF=AF=AB，
即AD+BC=AB.
练习册系列答案
相关题目
【题目】某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查，绘制出频数分布表和不完整的频数分布直方图，请根据图表信息回答下列问题：
初中毕业生视力抽样调查频数分布表
视力 | 频数（人） | 频率 |
4.0≤x＜4.3 | 20 | 0.1 |
4.3≤x＜4.6 | 40 | 0.2 |
4.6≤x＜4.9 | 70 | 0.35 |
4.9≤x＜5.2 | a | 0.3 |
5.2≤x＜5.5 | 10 | b |
（1）本次调查的样本容量为 ；
（2）在频数分布表中，a= ，b= ，并将频数分布直方图补充完整；
（3）若视力在4.6以上（含4.6）均属正常，根据上述信息估计全区初中毕业生中视力正常的学生有多少人？
